math

Experiencing MathReps Success at Cipriani Elementary

AdminLeave a comment

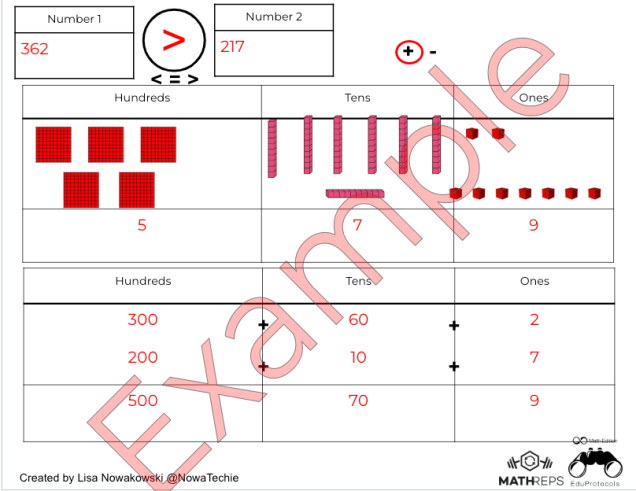
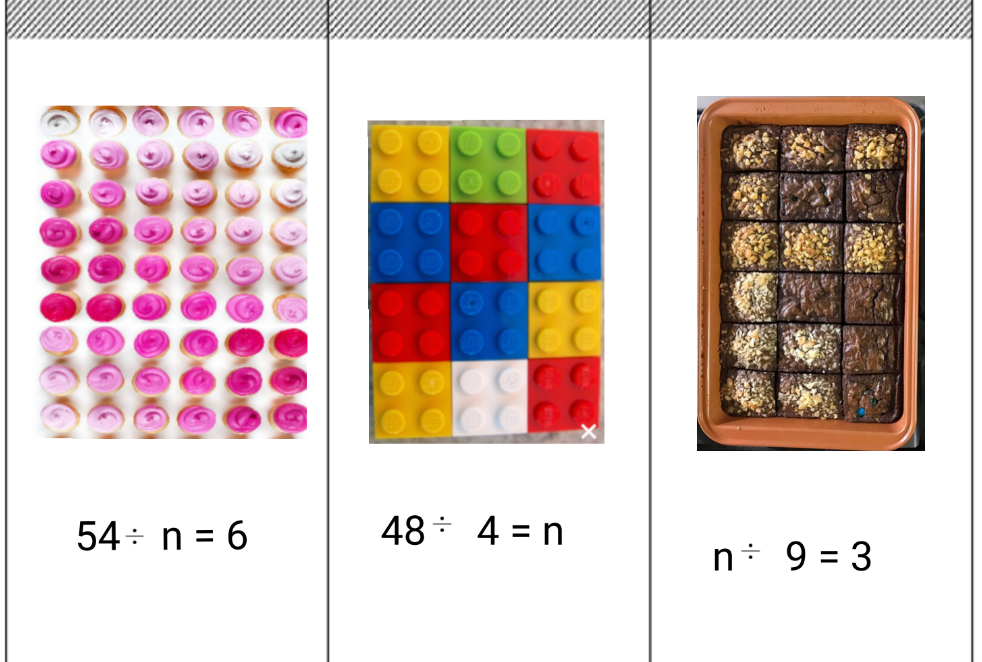
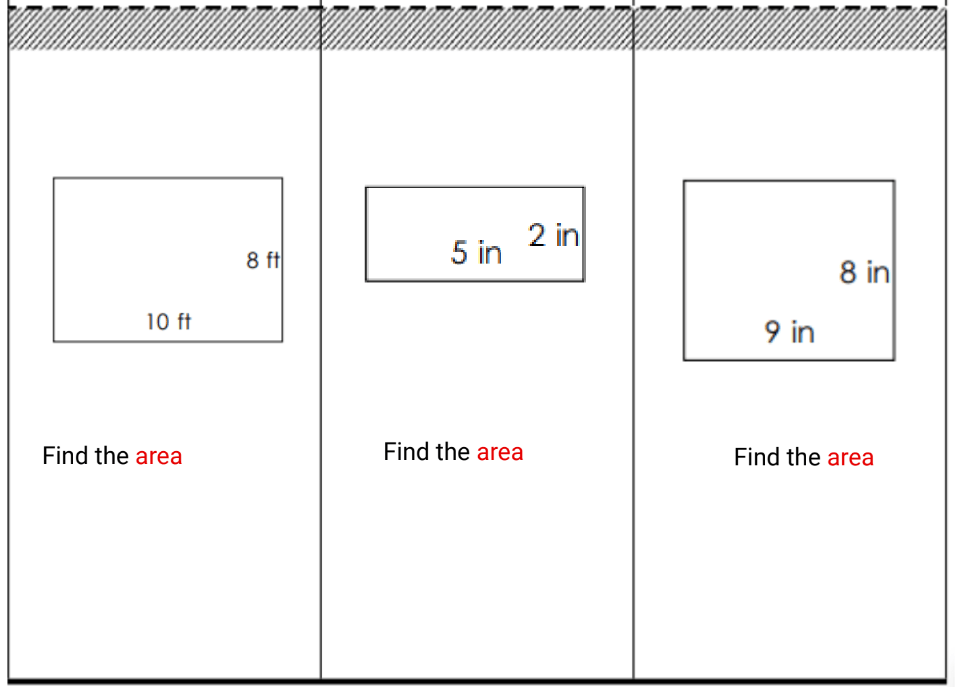
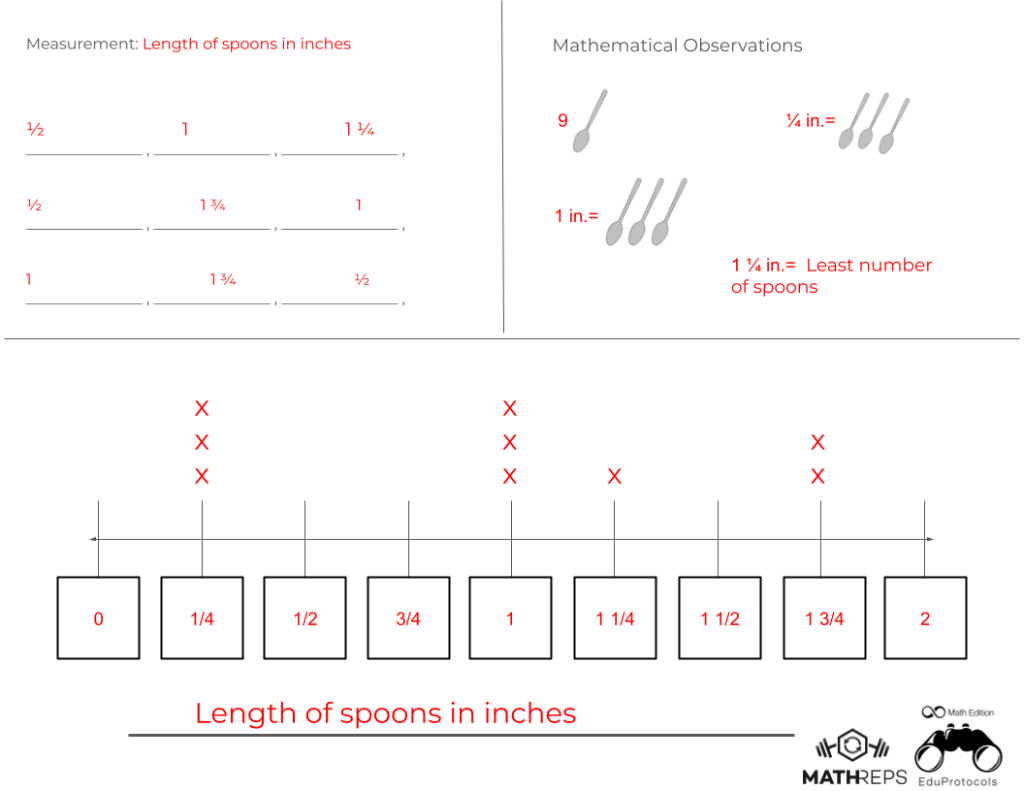
A few weeks ago, I had the absolute pleasure of visiting Cipriani Elementary School in Belmont, California, and let me tell you—it was a fantastic day that filled my heart.

Throughout the day, I was met with warm smiles, welcoming teachers, and the most amazing group of students. I had the opportunity to visit several classrooms ranging from TK through fifth grade, and in each room, I was able to demonstrate MathReps and watch in amazement as students flourished in their math knowledge.

What stood out most to me during these classroom visits was the level of engagement and understanding the students displayed. They were respectful, kind, curious, and so eager to learn. It’s one thing to talk about the power of MathReps—but it’s another thing entirely to see it in action in so many classes.

The Cipriani staff was incredible. Not only were they open and receptive, but they also shared their own tips and tricks for how they modify and adapt MathReps to meet the needs of their students. I was genuinely inspired by the way they’ve made the framework their own. I came to share—but I left having learned so much from them too. That kind of collaborative energy is what makes this work so meaningful.

One of my favorite moments from the day happened in a third-grade classroom. As I was working with the students, one of them looked up at me, wheels turning in their head, and said, “Wait… your name is on the bottom of our MathReps!” The class instantly lit up with excitement. Then they asked, “Did you also make Math Dash Chats?” When I said yes, the energy doubled. That little moment of connection—of realizing that the person who created something they use every day was standing right there with them—was truly special. It reminded me that kids are paying attention, even when we don’t think they are.

Later that afternoon, I led a Math 360 professional development session with the entire staff. Thanks to our friends at Wipebook, we had large Wipebook flip charts to work with, and it made the experience even more interactive and fun. The discussions were rich and reflective, and once again, the Cipriani teachers brought their full selves to the table—asking great questions, sharing insights, and showing a genuine passion for improving math instruction.

Overall, it was such a rewarding, joy-filled day. I left Cipriani Elementary feeling deeply grateful—and even more motivated to continue visiting classrooms across the country to share the love, importance, and power of MathReps.

I am thankful to everyone at Cipriani Elementary for making me feel so welcome.

Spice Up Your Math Lessons with the Nacho Problem EduProtocol!

AdminLeave a comment

Allow me to introduce you to an engaging and effective way to get your students thinking critically about math: Nacho Problem! If you’re looking for a structured-yet-flexible approach to problem-solving that promotes discussion, reasoning, and collaboration, then this EduProtocol is exactly what you need.

What is Nacho Problem?

Nacho Problem is a structured math discussion protocol that helps students develop their problem-solving and reasoning skills in a low-floor, high-ceiling way. Instead of just solving problems in isolation, students work through an incorrectly solved problem that leads to, explaining their thinking, and building deeper conceptual understanding.

It’s not just any problem—it’s “Nacho” Problem because it encourages students to engage with math differently!

How It Works

Nacho Problem follows a consistent routine that makes math discussions more meaningful and accessible for all learners. Here’s a breakdown of the process:

Launch the Problem:

  • Choose a problem that has been solved incorrectly. It can be a common misconception or a key concept.
  • Present the problem to the class and encourage students to think critically.

Think & Solve:

  • Students work independently or in pairs to solve the problem using their own methods.
  • They show their thinking through models, equations, or number lines.

Share & Compare:

  • Students explain how they solved it and compare their work with others.
  • Emphasize multiple strategies—there’s more than one way to solve a problem!

Debrief & Reflect:

  • Discuss which strategies were efficient, clear, or creative.
  • Make connections between representations and reinforce math vocabulary.

Why Use Nacho Problem?

🔹 Builds Math Confidence – Encourages all students to participate in math discussions.
🔹 Focuses Thinking – Students can critically analyze problems, looking for errors and correcting them.
🔹 Reinforces Multiple Strategies – Helps students see different ways to approach a problem.
🔹 Encourages Math Talk – Improves reasoning, justification, and communication skills.
🔹 Works with Any Grade Level – Can be adapted for K-12 by adjusting the complexity of the problem.

Hear About It In Under 2 Minutes

I recently created a video tutorial to show exactly how Nacho Problem works. Check it out here:

Try It in Your Classroom!

Want to give Nacho Problem a try? Here’s what you can do next:

Choose a problem that fits your students’ current math skills.
Use a template to help students structure their thinking.
Encourage collaboration by having students discuss and compare strategies.

You can find free templates and more math strategies at eduprotocolsplus.com and MathReps.com!

Final Thoughts

Nacho Problem is a fun, engaging, and powerful way to deepen students’ understanding of math. By making math conversations routine and structured, you’ll see more confidence, curiosity, and engagement in your classroom.

Understanding Subtraction with Pictorial and Expanded Models

AdminLeave a comment

Why Use Multiple Models?

By using a pictorial model alongside expanded notation, students get a visual and numeric understanding of subtraction. This helps them move beyond memorized procedures to truly grasp why and how regrouping works.

Let’s break it down step by step!

Step 1: Set Up the Problem

We’re working with 736 – 274.

  • 736 is represented using pictorial models in a place value chart:
    • 7 hundreds
    • 3 tens
    • 6 ones
  • Below, we note in the corner of each place value column what we’re subtracting: 200 + 70 + 4 = 274

Step 2: Subtract Using the Pictorial Model

Subtract the Ones (6 – 4):

  • Cross off 4 ones (I like to use x to represent 1s).
  • That leaves 2 ones.

Regroup the Tens (30 – 70):

  • Uh-oh! We don’t have enough tens to subtract 70.
  • So, we regroup 100 into 10 tens (since 100 = 10 tens).
  • Now, we have 13 tens total (13 tens = 130)
  • We subtract 70 (or 7 tens) from 13 tens, leaving 6 tens (or 60).

Subtract the Hundreds (700 – 200):

  • After regrouping, we have 600 left in the hundreds place.
  • Subtracting 200 leaves us with 400.

Final Answer: 462

Step 3: Solve Using Base 10 Expanded Notation

Now, let’s represent the numbers in expanded form:

  • 736 → 700 + 30 + 6
  • 274 → 200 + 70 + 4

Subtracting step-by-step:

  • 6 – 4 = 2
  • 30 – 70 (not possible, so we regroup from the hundreds)
    • Moving 100 over to the 10s place, making it 130 – 70 = 60
  • 600 – 200 = 400

Final Answer: 462

The Power of Dual Modeling

Using both pictorial and expanded form models side by side helps students see:
✏️ Why we “regroup” in subtraction
✏️ How place value plays a role in regrouping
✏️ That both methods lead to the same solution, reinforcing accuracy

When students see and practice both models together, they build deeper number sense and mathematical confidence!

Try This in Your Classroom!

You can grab a free MathReps template at MathReps.com and start using this strategy with your students today!

💡 Bonus Resource: Wipebook offers workbooks with four MathReps for second grade, providing structured practice all year long. Check them out!

Watch the Full Tutorial Video

Effective MathReps for Addition with Regrouping

AdminLeave a comment

Today, we’re diving into second-grade math with a MathRep that focuses on addition with regrouping.

In our previous posts, we explored using MathReps for addition and subtraction without regrouping. Now, we’re taking it a step further and tackling regrouping, helping students make the jump from pictorial models to expanded notation and the base 10 system.

So, buckle in—let’s get started!

Step-by-Step Guide: Regrouping with MathReps

Set Up the Numbers

For this example, we’re adding 682 + 234, and we’ll use a pictorial model to visually represent the numbers before transitioning into the expanded form.

Solve Using a Pictorial Model

1️⃣ Start with the Ones Place:

  • 2 + 4 = 6
  • No regrouping needed here, so we write 6 in the ones place.

2️⃣ Move to the Tens Place:

  • We add 8 tens + 3 tens = 11 tens, which equals 110.
  • Since 10 tens = 100, we regroup by circling ten tens and moving them into the hundreds place.
  • This leaves 1 ten (10) in the tens place.

3️⃣ Move to the Hundreds Place:

  • We now have 6 hundreds + 2 hundreds + 1 regrouped hundred = 9 hundreds.

Bringing it all together:
916

Transition to the Base 10 Model (Expanded Notation)

Now, let’s break it down using expanded form:

  • 682 → 600 + 80 + 2
  • 234 → 200 + 30 + 4

Adding the place values:

  • Ones: 2 + 4 = 6
  • Tens: 80 + 30 = 110 → Regroup into 100 + 10
  • Hundreds: 600 + 200 + 100 = 900

Total: 916

Alternative Thinking: Flexible Number Sense

Instead of regrouping immediately, students can leave the tens as 110 and think of the sum as:

800 + 110 + 6 = 916

This approach challenges students to see numbers flexibly before applying the standard algorithm, deepening their conceptual understanding.

Why This Works

MathReps provide a structured, visual approach that helps students bridge the gap between pictorial models and formal mathematical notation. By working through regrouping in different ways, students develop number flexibility and problem-solving confidence.

Get Your Free MathReps!

Want to try this in your classroom? Download your free MathRep template at MathReps.com and explore even more math resources.

💡 Bonus Resource: Check out Wipebook for workbooks featuring MathReps—each workbook includes four MathReps to last the entire year!

Watch the Tutorial Video

Subtraction Made Simpler With MathReps

AdminLeave a comment

I’m here to show you how MathReps can make subtraction practice easier and more engaging for your students. In our last post, we explored how to use a MathRep for addition, and today, we’ll focus on subtraction.

This step-by-step guide will show you how to use the MathRep template in your classroom, helping students bridge the gap between visual models and abstract concepts.

See this MathRep in action!

Set Up the Numbers

For this example, we’ll work with 658 and 234. The subtraction problem is set up in a pictorial model, where the number 658 is represented visually, and 234 is broken down into ones, tens, and hundreds to subtract from each place value.

Use a Pictorial Model to Subtract

In the pictorial model, each section represents a place value: ones, tens, and hundreds.

  • Subtract the ones:
    • Start with 8 ones and subtract 4.
    • Cross out or erase 4 ones, leaving 4 ones.
  • Subtract the tens:
    • Start with 50 tens and subtract 30 (3 groups of ten).
    • Cross out 3 groups, leaving 20 tens.
  • Subtract the hundreds:
    • Start with 600 hundreds and subtract 200 (2 groups of 100).
    • Cross out 2 groups, leaving 400 hundreds.

Combine the remaining values:
400 + 20 + 4 = 424

Transition to the Base 10 Model

Now, transfer the pictorial model into a base 10 model by writing the numbers in expanded form:

  • 658 → 600 + 50 + 8
  • 234 → 200 + 30 + 4

Follow the same subtraction process:

  • Subtract the ones: 8 – 4 = 4
  • Subtract the tens: 50 – 30 = 20
  • Subtract the hundreds: 600 – 200 = 400

Bring it all together:
400 + 20 + 4 = 424

Why This Works

This activity helps students make meaningful connections between the pictorial model and the base 10 system, reinforcing their understanding of subtraction and place value. By bridging these two models, students gain confidence in solving subtraction problems and build a deeper understanding of the math concepts.

Get Started Today!

Ready to bring this subtraction strategy to your classroom? Head over to MathReps.com to download your free MathReps template and explore more resources for effective math practice.

With MathReps, subtraction doesn’t have to be overwhelming. By providing students with a structured and visual approach, you’re setting them up for success in their math journey. Let us know how it works for your students!

Engage Students with 2nd Grade MathReps Activities

AdminLeave a comment

I’m excited to share how MathReps can transform daily math practice into a fun and engaging activity for your students. Whether you’re a seasoned teacher or just starting your journey, MathReps are a fantastic tool to build fluency and confidence in math concepts.

For today’s demonstration, let’s dive into a 2nd-grade MathRep and explore how you can use it in your classroom. This template can also be found on Wipebook Workbooks and Kami!

Blank 2nd grade MathRep for addition or subtraction
Filled in example of the 2nd Grade MathReps template using addition.

Step-by-Step Guide: Using MathReps in Your Classroom

1. Set Up the Numbers

For this example, we’re working with 237 and 422. Begin by deciding whether your students will add or subtract these numbers. For this demonstration, we’ll focus on addition.

2. Use a Pictorial Model

Start by setting up the numbers in a pictorial model.

  • Creating a 100’s chart will help students represent each digit in the numbers.
    • Each x will represent the ones (I prefer x’s over dots as it can become hard to distinguish individual dots)
    • Each l will represent the tens
    • Each square will represent the hundreds
  • Count the ones, tens, and hundreds in each number:
    • Ones: 7 ones + 2 ones = 9 ones
    • Tens: 30 tens + 20 tens = 50 tens
    • Hundreds: 200 hundreds + 400 hundreds = 600 hundreds

Add these values together:
659

3. Transition to the Base 10 Model

Once students understand the pictorial model, encourage them to transfer the information to a base 10 model by breaking down the numbers into expanded form:

  • 237 → 200 + 30 + 7
  • 422 → 400 + 20 + 2

Have the students add the expanded forms:

  • Add the ones: 7 + 2 = 9
  • Add the tens: 30 + 20 = 50
  • Add the hundreds: 200 + 400 = 600

Bring it all together:
600 + 50 + 9 = 659

Why It Works

This activity bridges the gap between pictorial models and abstract math concepts. Students not only practice addition but also develop a deeper understanding of place value and number decomposition.

Get Started Today!

Ready to try this out in your classroom? Visit MathReps.com to download your free MathReps template and discover more resources for math practice.

By using MathReps, you’re helping students build foundational skills in a way that’s both structured and engaging. Give it a try, and let us know how it works for your students!

Check It Out In Action!

2 New Video Series Coming: Google & Math

AdminLeave a comment

I’ve been diving into the world of videos lately, and it’s exhilarating to see the endless array of tutorials available at our fingertips. To contribute my own unique perspective, I’m launching TWO engaging series that I can’t wait to share with you. The first will unveil practical tips and tricks for using Google Tools effectively—because there’s always something new to discover! The second series will delve into math strategies tailored for both students and teachers, exploring everything MathReps has to offer. Get ready to enhance your skills and insights!

I’m not sure when these will launch, but know for certain that they will be showcased here. The first Google tool I will be looking at is Slides. I plan to look at different components and dig into them. The goal is to keep the videos quick and engaging. Personally, I hate watching longer videos for the one piece of information I am looking for. I feel that by creating several Quick Tips, viewers can learn what they need to, quickly. As you can see from the image here, I’ll be covering Word Art in one of the first episodes.

The series based on MathReps will contain information on MathReps, Math Eduprotocols, and other math strategies. Like the previously mentioned series, the videos will be bite-sized nuggets for viewers. I’m unsure when I’m starting that series, but I am just as excited to get it going. I have several thoughts: looking at MathReps and how to implement them, teacher tutorials on different math strategies we teach students and other helpful math tidbits.

  1. For Google Tools Series:
  • What’s one feature in Google Slides you’d love to master or learn a quick tip about?
  • Do you have a favorite Google Tool that you’d like to see covered in future posts or videos?
  1. For Math Strategies and MathReps:
  • Have you ever used MathReps in your teaching or learning? What’s been your experience?
  • What’s your go-to math activity that engages students most effectively?
  1. For Both Series:
  • Which series are you more excited for—the Google Tools or the MathReps and Strategies? Why
  • Is there a specific topic you’d like to see covered in either of these series? Share it here, and I’ll consider adding it!
  • Do you have any tips or shortcuts for Google Slides or math strategies that you’d like to share with others?

Clothesline Math: Engaging Students with Interactive Learning

AdminLeave a comment

For those unfamiliar with clothesline math, think of it as an interactive number line. Chris Shore is an outspoken champion of this hands-on teaching tool that helps students better understand Number Sense. This tool goes beyond placing numbers on a number line. It can be incorporated into most math concepts.

Earlier this year, I introduced a group of 3rd-grade teachers to this concept. We started with a relatively simple concept to acclimate the students to the task. I copied Kristen Acosta’s 2nd Base 10 activity. In it, students were given a card and were tasked with understanding the number being represented. The example below (Kristen Acosta) shows different ways the numbers were represented. The students were then placed in groups of 3-4 and ordered their numbers. Then, each group went to the large number line (literal clothesline stretched from one end of the room to the other) and placed their numbers on the class number line. The slip of paper was folded so that the number ‘hung’ on the number line. You can also use clothes pins to secure the numbers in place. This led to many rich discussions on placement and spacing.

Create Your Own

This was a huge hit with the students and teachers. This led to teachers asking for others. We found a multiplication activity (Kristen Acosta). Then teachers wanted division, area and perimeter. Try as I might, I couldn’t find anything online that was already created. This, then, led to me creating them. This became a labor of love.

Like other math resources I create, I looked at the standard and the framework when I created these. The division clothesline has various representations of division: standard form, number line, and images. In each the missing number could have been the quotient, dividend, or divisor. The missing number (n) is the number that is placed on the number line.

It took me a bit to decide how to approach the area/perimeter. Ultimately, I decided that students should find either the area or the perimeter. I made sure that the students were exposed to a variety of images and challenges in order to find each. Some had a missing side, others only gave two side measurements to find the area or perimeter of a rectangle.

Engaging Kids in Math: Using Play-Doh for Multiplication

AdminLeave a comment

This school year, I have had the privilege of collaborating with several 3rd-grade teachers. During one meeting, I shared an innovative idea from a 4th-grade teacher, Ben Cogswell. He introduced the use of Play-Doh to help his students understand multiplication through hands-on activities. I really like how he incorporated MathReps into this lesson. In the accompanying image, you can see students recording their findings in a MathReps, along with an instructional video they can reference for guidance.

Students using Play-Doh and MathReps to assist in their understanding of Multiplication and Division.

Fast forward a few months into 3rd-grade. While meeting with one of the groups, one teacher, Jensen Hall, was excited to share that she had purchased some Play-Doh for her students to use as they begin learning about multiplication. Then, about a week later, she sends me this message with images:

Message: I meant to send this to you earlier but I'm so excited about it I had to make sure I didn't forget again (sorry it's after hours). I introduced multiplication today using the play doh and it was a massive success! Such a great idea you shared!!
Students showing off their work.

Taking a closer look at the image, the red arrow points to where a student wrote out the problem on their desk. Using equal sets, students were able to model how to solve the problem. While the faces have been hidden, I can assure you that they were all smiling and clearly having a good time.

We all want our students to be excited and engaged with math. In the rush to fit everything into a school day—assessments, end-of-the-year testing, and much more—we often forget how to make learning fun and hands-on. Starting with concrete models is essential when teaching new skills like multiplication. Taking the time to begin with concrete models will ultimately save us time later and allow students to truly understand these foundational skills, setting them up for future success.

The story and images have been shared with permission from the teacher.

Let’s (Line) Plot Something

Image AdminLeave a comment

If you are a 3rd-grade teacher looking to engage students with the concept of line plots, you are not alone. The task of transferring data onto a number line may seem straightforward to adults, but for young learners, it can be quite challenging. The 3.MD.B.4 standard, a supporting cluster in the Common Core Standards, plays a substantial role in reinforcing the understanding of fractions and measurement. This means that as students delve into the world of line plots, they are simultaneously immersing themselves in the intricate connections between fractions on number lines, and measurement. It’s a perfect illustration of how math is both messy and beautiful, all intertwined in a way that connects to the real world.

Putting It All Together

Here is an example of what this integration could look like. This MathRep integrates the fractions on a number line and measurement. The information is collected in the upper left quadrant. Students then fill in the information on the line plot. In the upper right quadrant, they can record their mathematical observations. Much like in the previous blog post, the observations serve as a low-floor, high-ceiling activity—one that all students can access and be successful in.

Teacher Set Up

The MathRep method grants teachers flexibility. Its primary aim is to offer consistent learning experiences for students while minimizing the teacher's preparation workload. When implementing this approach, teachers can start by providing all the necessary data in the upper left quadrant and should ensure variation in the data to allow the line plot to start at different points. For example, if a line plot ranges from 0 to 2, it's beneficial to vary it so that it may start at 5 on one occasion and 9 on another. In 3rd grade, students typically work with whole numbers, halves, and fourths. However, the provided data may not always include fourths, so students should adjust the intervals accordingly. As students become proficient in recording data on a line plot, they can then be tasked with measuring objects, recording the data, and accurately placing it on the line plot. No matter where in the process you find yourself, be sure to encourage students to record all mathematical observations in the upper right quadrant.

Outcomes

The outcomes of this MathRep further build students’ number sense, understanding of fractions, measurement, and data interpretation. It also illustrates how math concepts are interconnected and can be taught together instead of isolated. Another simple yet powerful activity. Have you tried it yet? What are your thoughts?