Images

Why Manipulatives Matter Beyond Early Grades

Image Admin2 Comments

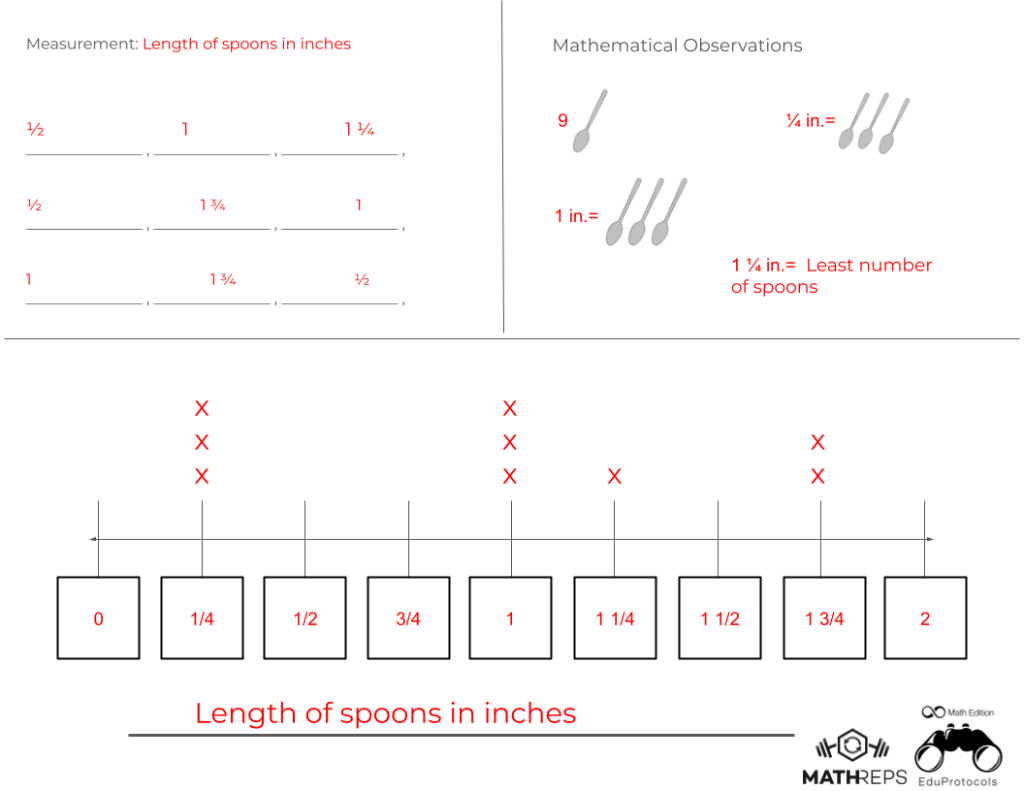
In the early grades, it’s not uncommon to see math manipulatives used daily in the classroom. Teachers pull out connecting cubes, counters, base ten blocks, and more—tools that help students build a concrete understanding of math concepts. Whether they’re exploring different ways to make 10 or practicing addition, these hands-on tools support their thinking in meaningful ways.

This follows the CRA model—Concrete, Representational, Abstract. We start with the concrete, like manipulatives. Once students have a solid grasp of the concept, we move into the representational, such as drawings or visual models. Finally, we introduce the abstract, using numbers and symbols alone. For example:

  • Concrete: Use connecting cubes to model 5 + 3
  • Representational: Draw 5 circles and 3 more
  • Abstract: Solve 5 + 3 = 8

But here’s what I’ve been thinking about lately: why do we often abandon manipulatives once students move into the upper grades?

Sure, by fourth or fifth grade, many students no longer need cubes for basic addition and subtraction. At that point, they’ve likely mastered those foundational skills and can work abstractly. But what about when we introduce new, more complex concepts—like volume in upper elementary or integers in middle school?

Volume is a great example. It’s a tough concept to grasp without something physical to hold or build. Yet so often, we hand students a formula and expect them to just “get it.” What if we instead gave them time to build with cubes, experiment, and see what volume means before jumping into the numbers?

The same goes for concepts like negative numbers. A number line or clothesline math activity can help students visualize and understand the relationships between positive and negative values. Why skip that step?

All this has me wondering: Is it a time issue? A training issue? Have we simply forgotten how powerful manipulatives can be for older students, too?

I’d love to hear your thoughts.
Do you use manipulatives in your classroom? What grade do you teach? What concepts do you use them for?

Let’s keep the conversation going—and keep math meaningful at every grade level.

Let’s (Line) Plot Something

Image AdminLeave a comment

If you are a 3rd-grade teacher looking to engage students with the concept of line plots, you are not alone. The task of transferring data onto a number line may seem straightforward to adults, but for young learners, it can be quite challenging. The 3.MD.B.4 standard, a supporting cluster in the Common Core Standards, plays a substantial role in reinforcing the understanding of fractions and measurement. This means that as students delve into the world of line plots, they are simultaneously immersing themselves in the intricate connections between fractions on number lines, and measurement. It’s a perfect illustration of how math is both messy and beautiful, all intertwined in a way that connects to the real world.

Putting It All Together

Here is an example of what this integration could look like. This MathRep integrates the fractions on a number line and measurement. The information is collected in the upper left quadrant. Students then fill in the information on the line plot. In the upper right quadrant, they can record their mathematical observations. Much like in the previous blog post, the observations serve as a low-floor, high-ceiling activity—one that all students can access and be successful in.

Teacher Set Up

The MathRep method grants teachers flexibility. Its primary aim is to offer consistent learning experiences for students while minimizing the teacher's preparation workload. When implementing this approach, teachers can start by providing all the necessary data in the upper left quadrant and should ensure variation in the data to allow the line plot to start at different points. For example, if a line plot ranges from 0 to 2, it's beneficial to vary it so that it may start at 5 on one occasion and 9 on another. In 3rd grade, students typically work with whole numbers, halves, and fourths. However, the provided data may not always include fourths, so students should adjust the intervals accordingly. As students become proficient in recording data on a line plot, they can then be tasked with measuring objects, recording the data, and accurately placing it on the line plot. No matter where in the process you find yourself, be sure to encourage students to record all mathematical observations in the upper right quadrant.

Outcomes

The outcomes of this MathRep further build students’ number sense, understanding of fractions, measurement, and data interpretation. It also illustrates how math concepts are interconnected and can be taught together instead of isolated. Another simple yet powerful activity. Have you tried it yet? What are your thoughts?

Measurement & Data Excite Me!

Image Admin1 Comment

When you think about data, the first thoughts that come to mind might be how dull or uninspiring it can be. But what if there was a way to turn that perception around and make learning about data an exciting journey for elementary school students?

Enter the newest MathRep. This template is designed to engage students while teaching bar graphs and picture graphs to young learners.

In this blog, we will delve into how this new MathReps template is exciting elementary math students. It offers educators a fresh and dynamic method to ignite enthusiasm for data interpretation among their students. Get ready to explore the possibilities and discover how this MathRep can make a real difference in the classroom!

Picture This

This is an example that aligns to 3rd-grade standards: 3.MD.B.3 Draw a scaled picture graph and a scaled bar graph to represent a data set with several categories. Solve one- and two-step “how many more” and “how many less” problems using information presented in scaled bar graphs.

You’ll notice that the same information is used to complete each of the graphs. This leaves quadrant 4. It can have questions about how many more and how many less, but why not allow students to observe the data and make their own observations. Leaving it open-ended like this allows all students to be successful. In addition, you will have students making observations that go beyond how many more/less.

The Setup

When first introducing this MathRep activity, it is recommended to provide students with the information located in the center of the paper. Subsequently, they can proceed to create the graphs themselves. Once they have gained proficiency in graph creation, the teacher can fill in the graph and task the students with completing the remaining sections, including the center. For a more advanced approach, the teacher can fill in the ‘Mathematical Observations’ square (quadrant 4), leaving the rest to the students. This adaptable strategy can effectively challenge students at various proficiency levels, guiding them toward a deeper comprehension of the material.

What Will You Do?

The power of this MathRep lies in its ability to enable students to interact with data in multiple ways simultaneously. This allows students the opportunity to make connections between different representations of information, leading to a deeper understanding. Teaching skills in isolation should and has been discontinued according to the Common Core Math Clusters, as math is intertwined with all aspects of learning. This MathRep illustrates these connections, preparing students for future success.

Number Paths for Students

Image AdminLeave a comment

Primary teachers have been embracing the concept of number paths as a valuable tool to foster fluency and number sense among young learners. A number path is a linear visual representation of numbers, which serves as a versatile aid in helping primary students comprehend and engage with numbers more effectively. As I have been collaborating with a group of primary teachers, it has become evident that they recognize the significance of number paths in facilitating a deeper understanding of numerical concepts. This has led to an increasing demand for additional number paths, reflecting the enthusiastic adoption of this resource within their educational practice.

Why?

After spending a few weeks working with small groups, the teachers quickly realized the potential of this tool for the whole class. They noticed an improvement in their students’ abilities, prompting another teacher to request number paths from 21 to 40 for practicing addition and subtraction with larger numbers. These number paths are completely customizable, so whatever your needs are, you’re covered.

Create

Initially, I created the prototype with cardstock, pipe cleaner/craft sticks, and a bead. That proved not to be the best. So, for the teachers, I laminated the cardstock, switched to a piece of yarn, and changed out the bead style. They work fantastically. I also made sure to take a piece of packing tape to the back to secure the yarn after it was knotted.

Result

It was a huge success! Students can easily manipulate the beads, allowing them to learn about numbers in a hands-on fashion. If you would like a copy of the templates, feel free to download them. They are in the Kinder and 1st-grade MathReps slide decks. I have also created some number path games that I will post about later this week.

How are you using number paths in your primary classrooms, and how are your students responding?

Download the template

Is a Parallelogram a Trapezoid?

Image AdminLeave a comment

I often find myself going down unexpected rabbit holes, and today was no exception. While on a quest to create a more engaging quadrilateral hierarchy for a 3rd-grade team, I found myself pondering the age-old question: Is a parallelogram a trapezoid? As it turns out, the answer is both yes and no!

I know. You’re wondering how it can be a trapezoid and yet not a trapezoid simultaneously. The answer lies in the definition of a trapezoid. The Oxford Dictionary defines a trapezoid as “a quadrilateral with only one pair of parallel sides.” So, according to this definition, the answer is no, which makes our math ‘program’ give incorrect information (that is a whole other post). However, many define it as a quadrilateral with at least one pair of parallel sides, which makes a parallelogram a trapezoid and our math ‘program’ correct.

In my math mind, a parallelogram is separate from a trapezoid. According to the hierarchy, the broad spectrum is quadrilateral. Below that there are either two or three main categories of quadrilaterals: kite, trapezoid, and sometimes parallelogram. Then, the parallelogram can be further broken down into rectangle and rhombus. Those can both be broken down into a square.

For the purposes of our district, I followed the current ‘curriculum’ where a parallelogram is a trapezoid. Below are the two variations of the poster.

So, what are your thoughts? Is a parallelogram a trapezoid or not?

MathReps Deliver Results

Image AdminLeave a comment

For years, I’ve questioned the effectiveness of MathReps and pondered whether the skills transferred to everyday math tasks. Known for overthinking and constantly questioning things, I’ve been intrigued by recent data from teachers showcasing the positive impact of MathReps on their students.

There are numerous reasons to celebrate these results. Firstly, this is a multi-year comparison illustrating a significant improvement. The 2024 year initially showed a much lower proficiency level than the 2023 year. However, it is important to note that their overall gains were greater in 2024. Secondly, the teaching staff remained consistent over these two years; there were no departures or new additions. Remarkably, one particular class saw an astounding increase from 5% to 90% proficiency in just 4 weeks. It’s worth noting that this exceptional progress happened after the teacher conducted the final assessment earlier than planned due to external circumstances. Subsequently, the same group of students took the SBAC IAB for Fractions, which resulted in 14% below the standard and 86% at or above it. This is particularly noteworthy as the class had only been 5% proficient with fractions a few weeks earlier. While the teacher deserves full credit, she acknowledged that regular completion of MathReps played a role in this achievement. Furthermore, the IAB takes the students’ knowledge of the subject matter and requires them to use that knowledge in context. This further supports knowledge transfer is happening. This is just one example of the success that can be achieved through the use of MathReps.

Why do I bring this up? Students are struggling, and teachers are noticing. Too often students come without the basic skills necessary to succeed with the expected standards. I witnessed this many years ago (pre-pandemic) and created the first MathRep. I noticed that my 5th-graders could master the expected skills during the first trimester. Then, the skill expectations shifted to fractions in the second trimester. This is where many of my students lost the skills they acquired in the first trimester. So by the time the third trimester rolled around, all was forgotten from the beginning of the year. Needless to say, this is less than ideal, especially when state testing is right around the corner. So MathReps were born!

So, after several years and an ever-growing library of MathReps I have started hearing from countless teachers from across the county witnessing the same success I am seeing with teachers in my district. I love that they also share stories about their students and how they have gained confidence through MathReps. All this is to say, if you haven’t tried them, you should!

What are MathReps?

MathReps are carefully crafted templates that incorporate interconnecting skills/standards. MathReps allows students to make connections between skills and concepts seamlessly. They are customizable and versatile. The repetition allows students to master the skills without the cognitive load of navigating a new ‘review page’ each day. The format remains the same. The teacher changes the number each day, allowing students to work through a series of skills. The teacher provides immediate feedback by walking around the classroom or checking the work as a whole, leaving zero paperwork for the teacher to deal with at the end of the day.

MathReps explanation video

Where to Start

With this data, it’s a no-brainer. MathReps work. If you’re looking to get started, head on over to MathReps.com and find a template that’s right for you! No need to worry about the cost, it’s FREE! The templates are all teacher-generated. That’s right, made by teachers just like you for students just like yours.

Ditch the C.U.B.E.S. Strategy in Math

Image Admin2 Comments

First of all, I want to acknowledge the tremendous impact of Robert Kaplinsky’s insights, which have resonated with many for years. His thought-provoking posts “Is Problem Solving Complex or Complicated?” and “Why Do We Have Word Problems?” are invaluable resources. Today, I want to not only express my appreciation for Kaplinsky’s work but also highlight an alternative strategy to the C.U.B.E.S. approach. We can broaden our problem-solving toolset by exploring new perspectives, and I believe this strategy will further enhance our problem-solving skills. Don’t miss out on the original posts: Is Problem Solving Complex or Complicated? and Why Do We Have Word Problems?.

This image shows what the acronym C.U.B.E.S. represents. Many teachers use this to teach an easy way for students can begin to tackle word problems. I, in fact, had an anchor chart displaying this very technique many years ago. As the saying goes, “Know better, do better.” I now know better and therefore do better. I know you might be asking yourself, “Okay, but I still don’t get why this isn’t ideal?”


Let’s consider the problem to the right. With our adult brains, we understand that it is a two-step problem. We understand we need to add the adults and children together and then subtract the number of males who were in attendance. Now imagine your 8-year-old self reading this and not yet having reading mastered let alone the comprehension skills to decode what is being asked. (Okay, maybe that was just me and my learning disability) You can see that I also went through the CUBES strategy. I circled the numbers, underlined the question, boxed keywords, and got rid of extra information. Arguably, the statement that everyone showed up might also be considered extra information to a young learner. An 8-year-old will start the CUBES process. They will look at the boxed words to find out what operation they need to use. And this is where we run into our first problem. It only says, “How many.” It doesn’t say, “how many more,” or “how many less.” Being around kids, we know that their default is to add. So what are they going to do? You guessed it, add 12, 25, and 15. Even if the question that is underlined is: How many females were there? chances are students are still going to add it all up because they are specifically looking for keywords like ‘in all’, ‘altogether’, ‘less’, ‘more’, etc.

Years ago, I used to teach my elementary students these strategies, as it was what I knew at the time. However, as I learned better strategies to help students, one of my favorite methods became the 3-Read Protocol. You can find more information about it in the blog post Mastering Mathematical Language Routine 6: Three Reads. This approach helps students concentrate on understanding the story, identifying units and quantities, and focusing on the question or task. By following the 3-Read Protocol, students can comprehend the context, which enables them to think critically instead of simply focusing on a procedure that may or may not work.

Finally, to help students effectively apply the information from the story, I highly recommend integrating MathReps into your classroom. MathReps are strategically practiced sets of skills that allow students to practice basic math concepts in similar skill clusters and receive immediate feedback. This approach promotes automaticity and fluency, freeing students to focus on what is needed rather than both what to do and how to do it. You can delve deeper into MathReps by reading a series of blog posts. I suggest starting with The Power of MathReps.

Magic School – UDL Choice Board

Image AdminLeave a comment

Earlier today, I had the pleasure of meeting with a fantastic group of teachers from Plymouth-Canton Community Schools in Michigan. Our main focus was on incorporating more EduProtocols and technology into math classes. During our discussion, we touched upon the topic of what students can do once they have demonstrated mastery using MathReps. Specifically, if students show mastery on their weekly assessment for two consecutive weeks, I no longer require them to do the daily practice in the following week. To provide an alternative avenue for these students, I suggested the use of a Choice Board, allowing them to delve deeper into the skills they have mastered. This idea sparked a conversation about the UDL Choice Board creator in Magic School. Intrigued by this resource (see previous post), I decided to explore this component further, and I must say, I was not disappointed.

After finding the Choice Board (UDL), I chose the grade level and input the standards. For my purposes, I chose all of 5.NBT. I gave the tool minimal parameters.

The output was okay:

Choice Board: Place Value and Decimals

AssignmentDescription
  1. Place Value Detective| Create a comic strip showing how a digit’s value changes based on its position in a multi-digit number.
  2. Decimals in the Real World| Research and create a slideshow presentation showcasing examples of decimals in everyday life.
  3. Powers of 10 Exploration| Design a poster explaining patterns in the number of zeros when multiplying or dividing a number by powers of 10.
  4. Decimal Number Line| Construct a number line using decimals and demonstrate how to compare decimals using greater than, less than, and equal to symbols.
  5. Rounding Riddles| Create a set of riddles where students need to round decimals to a specified place value to find the answer.
  6. Decimal Art Gallery| Use various art materials to represent decimals visually. Label and display your artwork in a mini gallery.
  7. Interactive Place Value Game| Develop a board game that involves using place value understanding to round decimals. Include instructions and game pieces.
  8. Decimal Number Chef| Write a step-by-step recipe using decimals for a favorite dish. Include appropriate measurements and conversions.
  9. Decimal Reflection| Write a reflective journal entry explaining the importance of understanding place value and decimals in real-world applications.

Remember to be creative and have fun with your chosen assignment! Additionally, ensure that your work demonstrates your understanding of place value and decimals.

But not very user-friendly. So, I modified my request. Not exactly what I wanted but much better visually. I would prefer if it were a 3 x 3 grid. I did put in the request unfortunately, the tool wasn’t able to create it. But the output was still good and easier to read. And if I really wanted a 3 x 3 grid, I could simply copy and paste the components:

Sure! Here’s the choice board in a 3 x 3 table format:

AssignmentDescription
1. Place Value DetectiveCreate a comic strip showing how a digit’s value changes based on its position in a multi-digit number.
2. Decimals in the Real WorldResearch and create a slideshow presentation showcasing examples of decimals in everyday life.
3. Powers of 10 ExplorationDesign a poster explaining patterns in the number of zeros when multiplying or dividing a number by powers of 10.
4. Decimal Number LineConstruct a number line using decimals and demonstrate how to compare decimals using greater than, less than, and equal to symbols.
5. Rounding RiddlesCreate a set of riddles where students need to round decimals to a specified place value to find the answer.
6. Decimal Art GalleryUse various art materials to represent decimals visually. Label and display your artwork in a mini gallery.
7. Interactive Place Value GameDevelop a board game that involves using place value understanding to round decimals. Include instructions and game pieces.
8. Decimal Number ChefWrite a step-by-step recipe using decimals for a favorite dish. Include appropriate measurements and conversions.
9. Decimal ReflectionWrite a reflective journal entry explaining the importance of understanding place value and decimals in real-world applications.

I hope this format is helpful for you and your students! Let me know if there’s anything else I can assist you with.

Can this be improved? Definitely! Did I invest a lot of time fine-tuning the tool’s parameters? No. However, considering the minimal effort I put in, the output turned out to be surprisingly good. Without a doubt, I wholeheartedly recommend Magic School! I remain a fan of this remarkable tool!

Magic School AI

Image AdminLeave a comment

The world of AI tools is vast and ever-evolving. Amongst the sea of options, one particular tool has caught my attention: Magic School. With a focus on teachers and schools, it offers a unique approach that sets it apart from the rest. Its comprehensive range of categories opens up exciting possibilities for integrating AI into different educational contexts. The best part? It comes in both a free and paid version, tailored to suit varying needs. Allow me to share an image of its advantages from their official website. Get ready to dive into a world of innovative possibilities!

Compare subscription options for Magic School

On the home page, you will find 66 different categories. Some examples of these categories include Math Spiral Review, Standards Unpacker, Sentence Starters, Text Leveler, and IEP Generator, among many others. As I was curious, I decided to take a closer look at the Standards Unpacker category. What caught my attention was the fact that it addresses the specific skills that students need to succeed, provides clear Learning Targets, and summarizes the standard. However, I found the Instruction and Assessment Plan section to be somewhat vague. Nevertheless, one interesting aspect is that you can go back to the tool and use that initial plan as a starting point to create a more detailed and thorough plan.

Standard: 5.NBT.A.1

Break Down Standard:

Skills: Recognizing place value in multi-digit numbers
Knowledge: Understanding how the value of a digit changes as it moves to the left or right in a number
Concepts: Place value, base-ten number system, positional notation

Define Expectations:
In this standard, 5th-grade students are expected to understand the concept of place value in multi-digit numbers. They should recognize that each digit in a number has a specific value determined by its position. Additionally, they should understand that the value of a digit in one place is 10 times greater than its value in the place to its right, and 1/10 of what it represents in the place to its left.

Formulate Learning Targets:
By the end of this standard, students should be able to:

-Identify the place value of digits in multi-digit numbers.
-Determine the value of a digit based on its position within a number.
-Describe the relationship between the value of a digit and its position.

Instruction and Assessment Strategies:
Use manipulatives, such as base-ten blocks, to help students visualize and understand the concept of place value.
Provide opportunities for students to explore and compare the values of digits in different positions within a number.
Use number lines and number charts to reinforce the concept and relationship of place value.
Engage students in problem-solving activities that require them to apply their understanding of place value.
Assess students' understanding through quizzes, worksheets, and real-life problem-solving tasks that involve place value.

Summarize:
In this standard, 5th-grade students are expected to develop a deep understanding of place value in multi-digit numbers. They should be able to recognize the value of each digit based on its position within the number and understand the relationship of each digit to its neighboring digits. Instructional strategies such as hands-on manipulatives, visual aids, and problem-solving activities can help students master this concept. Assessment strategies should include both formal and informal methods to gauge students' understanding and application of place value.

From my brief exploration, I believe that this tool has the potential to greatly assist teachers in working more efficiently. It eliminates the need for teachers to come up with learning objectives, develop grading criteria, and design lesson plans. Although AI should not replace all of a teacher’s work, it can certainly assist them in the more demanding tasks. Teachers will still have the ability to review and customize the generated outputs to suit their specific requirements. Overall, I am optimistic about the potential of this tool.

Winter Break Activities

Image AdminLeave a comment

Winter Break is just around the corner, bringing with it a well-deserved break from schoolwork. The question of whether to assign homework during breaks has always sparked debate. In my district, we are lucky enough to enjoy a generous three-week break. This extended period of downtime can be a blessing for students. To make the most of this time, I developed an exciting Winter Break Activity board and a Kindness Calendar, taking the opportunity to engage students in meaningful and enjoyable activities. It is important to note that these are optional.

  • Activity Board

As you explore the Activity Board, you’ll discover a variety of captivating activities that students can freely choose from. Completing just three out of the nine options is all it takes to participate! It’s important to note that these activities are not meant to be completed within a short 15-minute period. They are designed to be flexible, allowing students to engage either with or without the use of technology. Additionally, I’m thrilled to share that during the break, I received proposals from some students who were keen on pursuing alternative activities, and I happily accepted their ideas! When we reconvene after the break, I make sure to allocate dedicated time for students to showcase and present their remarkable projects.

The Kindness Calendar is a favorite among parents! I have received numerous expressions of gratitude from parents and guardians for this calendar. They particularly value the reminders to “clean your room” and “get along with your siblings ALL day.” Parents also appreciate the underlying concept of promoting kindness, gratitude, and appreciation. This calendar is really a gift for parents.

And did I mention that this is available in English and Spanish? Well, it is!

Template