Eduprotocols

The Pedagogy-First Mindset

AdminLeave a comment

As a Tech TOSA, teachers often come to me when they have a spark of an idea and need the right tool to bring it to life. Sometimes, they just need a reliable replacement for a tool they loved, like finding a new home for video discussions after Flip changed. My role isn’t to audit what’s in their “digital closet,” but to offer support and guidance as we navigate the “energy” of our classrooms together.

With the growing conversation around screen-time limits in districts like LA Unified, we have to be honest about what that energy looks like. When we stand side-by-side in a classroom where students are on a mandate for 90 minutes of adaptive software each week (45 minutes for math and 45 minutes for ELA), the room is often stagnant. It’s quiet, but is it the silence of deep thought or the silence of digital compliance?

The person who is doing the work is doing the learning.

The “Work” Litmus Test

I have a quote I live by in my own classroom: “The person who is doing the work is doing the learning.”

When we look at tech tools, the question isn’t “is this high-tech?” but “who is doing the heavy lifting?”

  • Compliance Tech: The software handles the logic and sorts the levels. The student is a passenger.
  • Creation Tech: Tools like Canva or Snorkl (which now hosts MathReps!) require students to be the drivers. In Snorkl, there is no passive learning; the student must articulate their thinking and record their process. That is the kind of “work” that leads to true learning.

The “Fluff” Tax vs. The Power of Fun

We all need to break the monotony sometimes. A fast-moving game like 99math or Wayground can be a fantastic way to build the fluency and basic facts students need before they can perform complex math. That “sprint” of excitement is a bridge to the next level of mastery.

The “fluff” tax happens when the game mechanics (like 20 minutes of boss battles in Prodigy) take up more brain space than the actual math. If the stimulation is a barrier to the standard rather than a bridge, it’s worth asking if it’s truly propelling them forward.

Making the Most of Mandated Minutes

We know the reality: many districts mandate 90 minutes a week for math and reading software. As a coach, I’m not there to push back on district policy, but to support teachers in navigating it. When I stand side-by-side with a teacher in a “stagnant” room, I like to ask four gentle, clarifying questions:

  1. Is the tool giving accurate information? Does the data on the screen reflect the growth (or struggle) you are seeing in the classroom?
  2. How do you know they are learning the material? If we closed the laptop right now, could they explain the “why”?
  3. Is this propelling them forward? Is this tool helping them master a Priority Standard, or just helping them finish a level?
  4. Who is doing the thinking?

Everyone will have a different take on it, and that’s okay. Some tools work better for some than others.

Final Thought

The goal of looking at pedagogy first isn’t to add a burden to the teacher. It’s to ensure that when we do use screens, whether it’s for a mandated block or a creative EduProtocol, the tech is helping them think, not just helping them finish.

Join the Conversation

How do you balance the “stagnant” mandated minutes with the “energetic buzz” of creation-based learning? Have you found a tool that actually reflects the growth you see in your small groups? Let’s talk about it in the comments.

The MathReps Manifesto: Ending the “Rent-a-Concept” Cycle in Math

AdminLeave a comment

For years, I followed the “Trimester Trap.”

In Trimester 1, we did the heavy lifting: number sense, multiplication, and long division. By Trimester 2, we moved on to “All Things Fractions.” By Trimester 3, we were classifying polygons and plotting data, all while keeping one eye on the looming state test.

But then, the “April Epiphany” hit. When I circled back to prepare for testing, I realized my students didn’t own the math from Trimester 1. They had merely “rented” it for the unit test and returned it.

The math was gone.

I knew I had to stop teaching in silos. I needed a way to keep every Priority Standard “warm” year-round.

The Inspiration: From Grammar to Graphs

The spark came from Jon Corippo’s 8 p*ARTS of Speech. I saw how a simple, repeatable routine could solidify complex grammar, and I thought: Why aren’t we doing this with Math?

When I sat down to create the very first template back in 2016, I called it Place Value Basics. I’ll be honest: I explicitly wrote in that blog post that what I came up with “isn’t nearly as fun” as Jon’s version. But the core mechanism, squeezing 9 to 11 different standards onto a single page and hitting them daily, was there.

The results in my 5th-grade classroom weren’t just “better”, they were transformative. What started as a personal survival strategy quickly spiraled. A friend in 1st grade asked for a version. Then 3rd grade. Then Kinder. Suddenly, we weren’t just doing “reps”, we were building a movement.

Why Repetition Isn’t a Dirty Word

There is a common fear in modern education that any form of repetition is “drill and kill” – a soul-crushing exercise in flashcards that kills a student’s love for math.

But true MathReps are the exact opposite of a drill sheet.

  • Drill and Kill is 50 problems of the exact same skill, practiced in a vacuum until the brain shuts off.
  • MathReps is one number or set of numbers, run through 10 different connecting skills, practiced daily until the brain turns on.

We aren’t asking students to do the same thing over and over to get “fast.” We are giving them a predictable routine so their cognitive load is reduced. When they don’t have to worry about the format or “What do I do next?”, they finally have the mental space to notice patterns and ask “Why does this work?”

The Accidental Algorithm

I watched this play out beautifully with a 5th grader working on a MathRep that included the area model for division. In our conceptual progression, we weren’t teaching the traditional algorithm yet (that’s a 6th-grade standard); we were focusing on the “why” of place value blocks and area.

Day after day, this student engaged with the routine. Because he knew the structure inside and out, he stopped worrying about the instructions and started noticing patterns. One afternoon, he called me over, and I noticed his paper and inquired about his use of the algorithm.

“I saw that when I was doing it the other way, I could just figure out how many groups I needed from each place.”

Without a single direct instruction lesson, he had inherently figured out the traditional long division algorithm. He didn’t find it because he memorized an abstract chant or an acronym. He found it because the daily, low-stakes repetition of the area model allowed him to see the mathematical patterns so clearly that the traditional algorithm became the next logical step.

That is exactly how math is supposed to work: naturally, through curiosity and pattern-finding.

Rooted in the Classroom, Not a Boardroom

One thing that makes MathReps different is that it’s grassroots. This isn’t a framework developed by a textbook company or a corporate suite; it’s an educator-owned project born directly from the needs of real students in a real classroom. It’s built by teachers, for teachers, and refined by the feedback of the thousands of you who use it every day.

We now know the cognitive science backs this up. The 10-Minute Mastery Loop proves that daily mixed spaced retrieval beats the weekly review cycle every single time. If you only teach fractions in January and February, the brain flags that information as “temporary.” But if you touch a fraction every morning, the brain recognizes it as “essential.”

Where We Are Going Next

MathReps is no longer just a collection of legacy slides. As we look forward, our focus is on:

  • Universal Access: Expanding the searchable directory so you can find the exact standard you need in seconds.
  • Student Agency: Using the Number Menu to let kids bring their own real-world numbers into the math routine.
  • Sustainability: Keeping the “low-prep, high-impact” promise that makes this routine actually doable on a rainy Tuesday in February.

The “Manifesto” is this: Every student deserves to feel like a “Math Person.” By giving them a consistent routine to practice the Priority Standards of their grade level, we move math from short-term memory to long-term mastery.

Join the Conversation

We’ve all seen the “Trimester Trap” in action.

Which specific standard or concept do your students always seem to “return to the rental shop” by the time spring testing rolls around? Drop it in the comments, and let’s look at which MathRep can help you keep it warm!

The Power of the “Number Menu” in MathReps

Admin1 Comment

We’ve all been there. It’s your math block, and you’re asking students to run a Place Value MathRep. You need a number to work with. You could ask a student for a random number, and depending on your class, that could be dangerous. 6-7 anyone?

But what if we gave them a Menu instead?

The Number Menu is a simple, low-prep strategy to turn a standard MathRep into a high-interest, culturally relevant experience. By providing a curated list of 5–10 real-world numbers, you give students agency, choice, and a reason to care.

Why it Works

  • Natural Differentiation: Include a “Mild, Medium, and Spicy” option. A teacher can put a 2-digit, 4-digit, and 7-digit number on the same menu, allowing students to self-select their challenge level.
  • Connection: It bridges the gap between the classroom and the community.

Build Your Menu: 5 Categories to Get Started

You don’t need to reinvent the wheel every day. Pick a few categories, update the numbers once a week, and post them in a dedicated corner of your whiteboard.

1. The “Home Base” (Local Landmarks)

Perfect for place value, rounding, and measurement.

  • The School’s Address: Use the street number of your building or a famous local landmark (local library, coffee shop, or grocery store).
  • Local Elevation: What is the altitude of your town? A nearby town? (Great for comparing numbers!) You could even do the population!
  • The Distance: How many miles is it from your classroom to the nearest State Capital? Or city hall?

2. The “Scoreboard” (Sports Stats)

Sports are a universal language for engagement.

  • The Box Score: Points scored, total rushing yards, or the attendance at last night’s local or national game.
  • Jersey Math: Use the numbers of local high school stars or professional athletes. This is perfect for the 4 operations with double-digit numbers.
  • Pro-Tip: Don’t be afraid to be a “homer”! Why not use at least one Detroit Lions stat on the menu? What a great way to engage in math! Not a Lions fan? (Why not? – don’t answer that), Use a favorite team of yours or your students.

3. The “Main Street” (Community Math)

Connecting math to the economy that students see every day.

  • Price Points: The current cost of a gallon of gas or a local favorite “Happy Meal.”
  • Elapsed Time: If the local library opens at 10:00 AM and closes at 6:00 PM, how many minutes is it open?
  • Historical Age: The year your town was founded vs. the current year.

4. The “Trend” Report (Pop Culture & Digital)

Meeting students where they live—online.

  • The Viral Count: Use the view count (in the millions!) of a trending (and school-appropriate) video or song.
  • Gaming Stats: The current “active player” count for games like Minecraft.
  • The Countdown: How many days/hours until the next big movie release? Or a local event like the Salinas Valley Fair?

5. The “Wildcard” (Nature & Science)

For the kids who love the “did you know” facts. I love this idea. So many random

  • The Weather: Today’s high and low temperatures (perfect for introducing negative numbers).
  • Animal Facts: The weight of a local species vs. an exotic one (e.g., a Black Bear vs. a Blue Whale).

Keep it Simple

The goal of MathReps is to keep the routine stable so the thinking can be deep. You don’t need a fancy tech integration for this. A simple “Weekly High Five” list on the board is all it takes to transform a routine repetition into a meaningful conversation.

When you bring the world into your MathReps, you aren’t just teaching place value—you’re showing students that math is happening all around them.

What numbers or topics are on your menu this week?

Poster Template

The Spring Lifeline: Zero-Prep, High-Impact Math Review

AdminLeave a comment

It’s the end of April. If you’re like most teachers, you’re spent. Your students are spent. But the learning doesn’t stop just because the calendar flipped.

How do we keep the “polish” on our math skills without adding more prep to an already overflowing plate?

The “Assign and Go” Solution

I am thrilled to share that MathReps are live and pre-made inside the Snorkl library. No more standing at the copier. No more hunting for the right PDF. You can quite literally “Assign and Go.” Whether you need to sharpen the 4 operations or dive deep into fraction models, the heavy lifting is already done for you. And what a relief that is!

Why This is a Game-Changer Right Now:

  1. Zero Prep: Navigate to the Snorkl Library, click “EduProtocols,” and select “MathReps.” Everything from Kinder to 4th Grade (with 5th Grade coming soon!) is ready to push out to your students instantly.
  2. The AI Co-Teacher: At this point in the year, you don’t have the bandwidth to listen to 30 individual explanations. Snorkl’s AI does it for you. It listens to the student’s logic, catches the “Instructional Debt” (like that hidden skip-counting), and provides immediate feedback. Although you may have to remind the students to review the feedback, I’m finding that in some younger grades.
  3. Consistency Over Novelty: Since these are based on the MathReps your students already know, you aren’t teaching a new tool; you’re just using a better engine to run the routine.

How to Find Them:

It couldn’t be easier.

  • Log into Snorkl.
  • Navigate to the Library.
  • Look for the EduProtocols section.
  • Select MathReps.

A Quick Update for 5th Grade

I know my 5th-grade teachers are waiting. I’m currently getting those frames ready for you! Stay tuned; they’ll be live in the library soon to help you finish the year strong.

The Bottom Line: You don’t have to choose between your sanity and your students’ growth. Let Snorkl handle the prep and the feedback so you can focus on being the human connection your students need as we close out the year.

15-Day Routine for Math Test Confidence

AdminLeave a comment

In the sports world, athletes don’t spend the week before a championship learning new plays. They spend it “polishing”, perfecting their form, sharpening their reaction time, and ensuring their fundamentals are second nature. However, as a lifelong Detroit Lions fan, I’m not sure this analogy is always accurate. While I love my Lions, there have been plenty of games where it looked like they just learned the plays in the huddle! But all joking aside, as educators, we are preparing our students for life skills, not just a state test.

The Problem: The “Skill Blur”

When students are sitting at a computer, facing math problems one after another, cognitive overload is a real threat. The “how and when” of the four operations can easily get jumbled with fraction rules, and suddenly, all that geometry vocabulary becomes one big ole mess in their heads. This can be frustrating for both students and teachers.

It’s not that they didn’t learn the material; it’s that the retrieval is getting blocked by the sheer volume of information and tasks that need to be completed.

The Solution: MathReps as a Tactical Warm-Up

MathReps lower the affective filter by repeatedly practicing these core skills. I remember a year when my students didn’t just “do a unit” on decimals; we consistently spiraled decimal practice into our MathReps alongside other skills.

Because it was part of their regular routine, when they eventually faced a screen with decimal problems and tasks at the end of the year, they didn’t panic. The decimal didn’t throw them because it wasn’t a “guest star” in the curriculum; it was a familiar friend. By using MathReps as a 10-minute daily “Tactical Warm-Up,” we help students:

  1. Filter out the Format: They’ve seen the area model and the number line hundreds of times. The “test screen” is just another canvas for their existing skills.
  2. Sharpen the Fundamentals: We move from “manual labor” math to automaticity.

The 15-Day “Polishing” Routine

If you have 15 days left before the test, don’t reach for a packet. Reach for a Routine or EduProtocol.

  • The Selection: Pick the MathRep that addresses the skill your students find the weakest. If they are tripping over the arithmetic, use an Operations Frame (like the giraffe example below).
  • The Routine: Use the same MathRep at the beginning of your math period for at least one week. Consistency beats variety here. On Day 1, they are reacquainting themselves with the procedures; by Day 5, they are mastering the logic.
  • The Pivot: After 5 days, if you’re feeling good, move to another high-leverage frame. Or, cycle back to a different MathRep you used earlier in the year to keep those older skills from getting lost in the sauce.

The Bottom Line

We aren’t “cramming” for a test; we are clearing the fog. When we polish these skills through MathReps, we give students the confidence to show what they actually know, rather than getting lost in the “mess” of a testing interface and the information overload that bogs them down.

Snorkl + MathReps = Powerful Learning Moments

AdminLeave a comment

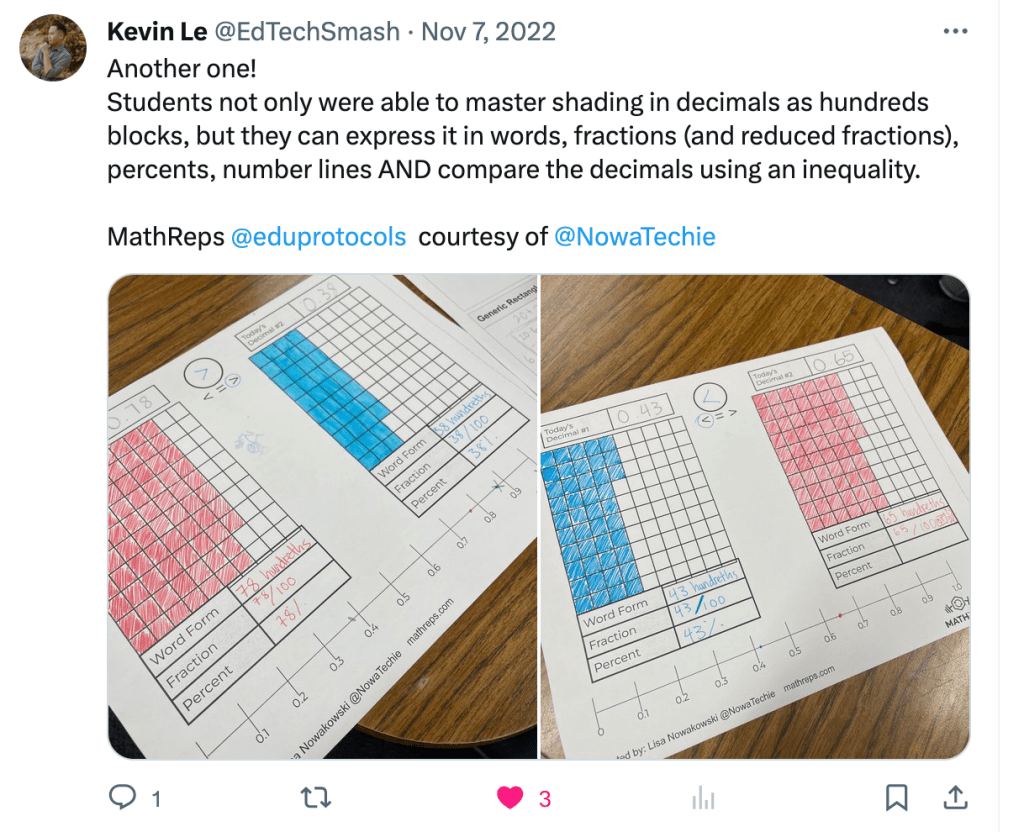
I’m sure I’ve mentioned Snorkl before, but it’s worth sharing again, especially because MathReps are part of the platform!

If you haven’t explored it yet, Snorkl is an AI-powered feedback tool that provides students with meaningful and personalized responses to their work. Teachers can create their own assignments or choose from Snorkl’s library of ready-to-go activities. These activities span all grade levels and subject areas – from kindergarten through high school – and include math, ELD, science, history, and language arts.

When a student completes an assignment, Snorkl analyzes their work based on the rubric (which it can even create for you!) and provides feedback and a score. It doesn’t provide answers, but instead encourages students to think deeper and revise their work.

A few reasons I ❤️ Snorkl:

  • It’s simple (not loaded with bells and whistles) and intuitive for both teachers and students.
  • Teachers can start from scratch or choose from a library of quality tasks.
  • Feedback can be provided in multiple languages, but teachers always see it in English.
  • Directions and feedback can be read aloud, making them perfect for young learners or multilingual students. (And it doesn’t sound robotic!)

Snorkl in Action: A Classroom Story

Recently, I had the opportunity to visit a 3rd-grade class to help them get started with Snorkl. (Total aside, but the teacher—Erin Daines—is one of the most naturally gifted educators I’ve ever met. I always learn something new in her classroom!)

On the first visit, we started simple with a fun activity from the Snorkl Library: “Introduce yourself and draw a picture of something you like.”

It was a low-stakes way for students to explore some of the whiteboard tools—pen, highlighter, shapes, and lines and get comfortable with the platform. We set it up so they could view and comment on one another’s work, and the engagement was instant. The room was buzzing with creativity and laughter.

When I returned the next week, we took things a step further. We made the next assignment collaborative, which meant students appeared under playful names, such as Zany Zebra or Curious Coyote. This anonymity helped students focus on ideas instead of popularity, something I really appreciate.

We started with a Would You Rather prompt: “Would you rather have a caramel apple or a slice of pumpkin pie?”

Students had to choose one and explain why. One student chose “neither” and explained his reasoning. Snorkl acknowledged his logic but scored it lower and challenged him to pick one, since the task was to make a choice, an excellent learning moment in a safe environment.

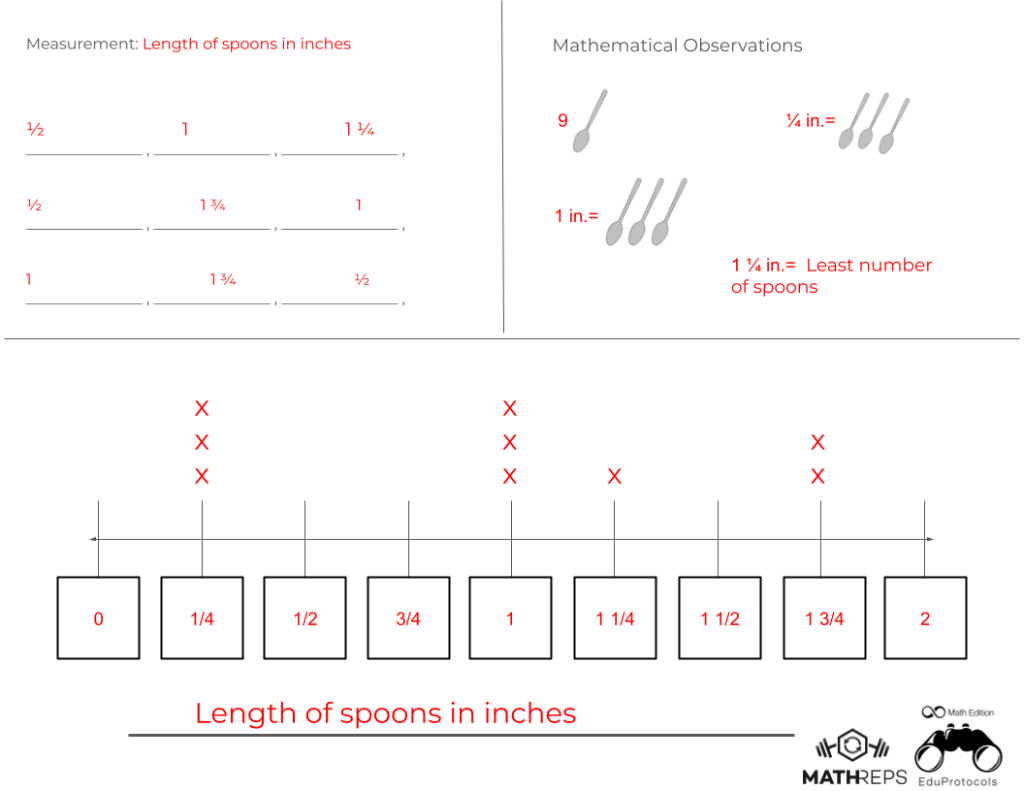
Then came the highlight: a 3rd Grade MathReps addition activity in Snorkl!

Students completed the task, then recorded their explanations to show their thinking. We know that when students can explain a process, their understanding deepens. Snorkl provided instant, helpful feedback that supported this reflection.

The best part? When students didn’t earn a 4/4, they wanted to improve. They read or listened to the feedback and tried again: some two or three times! The combination of MathReps and Snorkl fostered perseverance, reflection, and a sense of pride in learning. It was so exciting to witness.

Try MathReps in Snorkl!

Yes, MathReps are live in Snorkl—you’ll find them under the EduProtocols section. Currently, activities are available for grades K–4, with additional 4th-grade content and upper-grade levels forthcoming.

If you’d like to beta test upcoming MathReps in Snorkl, I’d love to have you join in! Just reach out and let me know.

So go ahead—try a MathRep in Snorkl. Let your students explore, explain, and shine.

Experiencing MathReps Success at Cipriani Elementary

AdminLeave a comment

A few weeks ago, I had the absolute pleasure of visiting Cipriani Elementary School in Belmont, California, and let me tell you—it was a fantastic day that filled my heart.

Throughout the day, I was met with warm smiles, welcoming teachers, and the most amazing group of students. I had the opportunity to visit several classrooms ranging from TK through fifth grade, and in each room, I was able to demonstrate MathReps and watch in amazement as students flourished in their math knowledge.

What stood out most to me during these classroom visits was the level of engagement and understanding the students displayed. They were respectful, kind, curious, and so eager to learn. It’s one thing to talk about the power of MathReps—but it’s another thing entirely to see it in action in so many classes.

The Cipriani staff was incredible. Not only were they open and receptive, but they also shared their own tips and tricks for how they modify and adapt MathReps to meet the needs of their students. I was genuinely inspired by the way they’ve made the framework their own. I came to share—but I left having learned so much from them too. That kind of collaborative energy is what makes this work so meaningful.

One of my favorite moments from the day happened in a third-grade classroom. As I was working with the students, one of them looked up at me, wheels turning in their head, and said, “Wait… your name is on the bottom of our MathReps!” The class instantly lit up with excitement. Then they asked, “Did you also make Math Dash Chats?” When I said yes, the energy doubled. That little moment of connection—of realizing that the person who created something they use every day was standing right there with them—was truly special. It reminded me that kids are paying attention, even when we don’t think they are.

Later that afternoon, I led a Math 360 professional development session with the entire staff. Thanks to our friends at Wipebook, we had large Wipebook flip charts to work with, and it made the experience even more interactive and fun. The discussions were rich and reflective, and once again, the Cipriani teachers brought their full selves to the table—asking great questions, sharing insights, and showing a genuine passion for improving math instruction.

Overall, it was such a rewarding, joy-filled day. I left Cipriani Elementary feeling deeply grateful—and even more motivated to continue visiting classrooms across the country to share the love, importance, and power of MathReps.

I am thankful to everyone at Cipriani Elementary for making me feel so welcome.

Let’s (Line) Plot Something

Image AdminLeave a comment

If you are a 3rd-grade teacher looking to engage students with the concept of line plots, you are not alone. The task of transferring data onto a number line may seem straightforward to adults, but for young learners, it can be quite challenging. The 3.MD.B.4 standard, a supporting cluster in the Common Core Standards, plays a substantial role in reinforcing the understanding of fractions and measurement. This means that as students delve into the world of line plots, they are simultaneously immersing themselves in the intricate connections between fractions on number lines, and measurement. It’s a perfect illustration of how math is both messy and beautiful, all intertwined in a way that connects to the real world.

Putting It All Together

Here is an example of what this integration could look like. This MathRep integrates the fractions on a number line and measurement. The information is collected in the upper left quadrant. Students then fill in the information on the line plot. In the upper right quadrant, they can record their mathematical observations. Much like in the previous blog post, the observations serve as a low-floor, high-ceiling activity—one that all students can access and be successful in.

Teacher Set Up

The MathRep method grants teachers flexibility. Its primary aim is to offer consistent learning experiences for students while minimizing the teacher's preparation workload. When implementing this approach, teachers can start by providing all the necessary data in the upper left quadrant and should ensure variation in the data to allow the line plot to start at different points. For example, if a line plot ranges from 0 to 2, it's beneficial to vary it so that it may start at 5 on one occasion and 9 on another. In 3rd grade, students typically work with whole numbers, halves, and fourths. However, the provided data may not always include fourths, so students should adjust the intervals accordingly. As students become proficient in recording data on a line plot, they can then be tasked with measuring objects, recording the data, and accurately placing it on the line plot. No matter where in the process you find yourself, be sure to encourage students to record all mathematical observations in the upper right quadrant.

Outcomes

The outcomes of this MathRep further build students’ number sense, understanding of fractions, measurement, and data interpretation. It also illustrates how math concepts are interconnected and can be taught together instead of isolated. Another simple yet powerful activity. Have you tried it yet? What are your thoughts?

Mastering Mathematical Language Routine 7: Compare and Connect

Image AdminLeave a comment

In the previous Mathematical Language Routine (MLR) discussions, we explored a variety of essential skills. MLR 1 focused on enhancing our understanding by revisiting and reinforcing key concepts, making our knowledge “Stronger and Clearer Each Time.” We then moved on to MLR 2, where we delved into the crucial skill of “Collecting and Displaying” data effectively. Building on this foundation, MLR 3 emphasized the importance of “Critiquing, Correcting, and Clarifying” our models and methodologies for optimal results. In MLR 4, we explored the “Information Gap” and how to use this strategy to be thoughtful of the information needed to solve problems. Continuing this journey, MLR 5 introduced the skill of “Co-Crafting Questions and Problems” collaboratively to foster innovative approaches and insights. Finally, in MLR 6, we explored the technique of “Three Reads,” emphasizing the significance of multiple reads in order to enhance student understanding. Let’s now embark on our next MLR discussion, MLR 7 Compare and Connect.

MLR 7: “Compare and Connect,” has the purpose of fostering students’ meta-awareness in their exploration of different mathematical approaches, representations, concepts, examples, and language. Through this MLR, students are encouraged to reflect on and verbally respond to these comparisons. This involves analyzing why certain mathematical actions or statements are done in a particular way, identifying and explaining connections between various mathematical representations or methods, and pondering how one idea relates to others in terms of both concepts and language. To support this learning process, teachers should model their thinking aloud when addressing these questions. This routine allows students to engage in rich mathematical conversations. We will explore two ways in which to accomplish this.

Which one doesn't belong

Getting students to engage in discussions about math, make connections, and consider different perspectives can be quite challenging. I often encounter students who simply say, “It was in my brain” or “My brain told me the answer.” However, by modeling and encouraging metacognitive awareness, students can begin to make connections on their own. One effective routine that focuses on linguistic skills is called ‘Which One Doesn’t Belong‘. This activity can be done in groups, in pairs, or as a whole class. Students are presented with four images, equations, numbers, graphs, or geometric shapes, and they are asked to identify a commonality among three of them and explain their reasoning. The interesting twist is that any combination of three out of the four options can be correct. For example, in the orange example, one could argue that the three triangles go together and the hexagon is the odd one out. Alternatively, one could justify grouping all the white-filled shapes while excluding the shaded shape. This activity is both enjoyable for students and provides the opportunity to hear and consider different viewpoints.

Another interesting activity that aligns well with this MLR is the Math EduProtocol Sous Chef from The EduProtocols Field Guide Math Edition (Chapter 9, page 56). In this activity, students are grouped together to solve a problem using different approaches and then present their work to the class. For instance, if students were given the task of solving 4 x 6 in third grade, one student might use equal groups, another could opt for repeated addition, a third student may create an array, while the last student represents the equation with the area model. Through this activity, students can establish connections with previously learned concepts and broaden their understanding. There are numerous ways to implement Sous Chef, but the central focus remains on fostering connections among ideas and encouraging students to share their thought processes orally.

In conclusion, incorporating this MLR into your math class will greatly benefit your students. It will help them enhance their meta-awareness, make connections between different concepts, and foster a deeper understanding of the subject. While we have explored two approaches to this MLR, there are numerous other equally powerful techniques available. In our next discussion, we will delve into MLR 8: Discussion Supports, which focuses on stimulating rich and meaningful conversations in the classroom.

Mastering Mathematical Language Routine 5: Co-Craft Questions and Problems

Image Admin1 Comment

In this ongoing blog series on Mathematical Language Routines (MLRs), we have covered four essential routines so far. Let’s recap their key ideas: MLR 1: “Stronger and Clearer Each Time,” MLR 2: “Collect and Display,” MLR 3: “Critique, Correct, Clarify,” and MLR 4: “Information Gap.” These routines are designed to enhance oral and written communication skills in mathematics. Now, let’s turn our attention to MLR 5: “Co-Craft Questions and Problems,” which offers a unique approach. It encourages students to actively participate in the question and problem-solving process, enabling them to explore mathematical contexts before seeking answers.

In MLR 5, students are given the opportunity to dive deeper into problem-solving by creating, analyzing, and enhancing mathematical questions, problems, and situations. The purpose of this routine is to provide students with a space where they can generate, analyze, and improve their understanding of mathematical concepts, specifically word problems. Through engaging in conversations, students refine their ability to formulate, select, and refine questions, allowing them to develop stronger critical thinking skills. This routine fosters students’ ability to use conversation skills effectively in the process of formulating, selecting, and refining their mathematical questions and problems. By actively participating in these conversations, students take ownership of their learning and become more proficient problem solvers. Curiosity Creator, found in The EduProtocols Field Guide Math Edition, Chapter 18, is one way to practice this routine.

Another excellent routine that can be seamlessly integrated into MLR 5 is the 3-Act Math Task, originally developed by Dan Meyer. This ingenious task involves providing students with minimal information, serving as a catalyst to foster curiosity and encourage them to generate questions that they can later answer with additional information provided in subsequent acts.


The first act, known as Act 1, is designed to stimulate students’ observation skills and curiosity. During this phase, students are encouraged to ponder upon what they notice and wonder about the given scenario. They also formulate questions that they will eventually solve. Act 1 is an opportune moment for students to engage in conversations regarding their observations, estimations ( too high, too low, or actual), a specific focus question, and the type of information they need to answer their own question.


In Act 2, students are provided with the necessary information to solve the problem or question they crafted in Act 1. Armed with this newfound knowledge, they embark upon the solving process.
Finally, Act 3 allows students to review the actual answer and assess whether their initial predictions were correct.

This routine is highly engaging for students across all levels, offering a perfect balance between accessibility and challenge. It also offers a wide range of ready-made, standards-aligned tasks suitable for students from Kindergarten through high school. By incorporating the 3-Act Math Task routine into the classroom, instructors can empower students to actively participate in problem-solving, develop critical thinking skills, and cultivate a deep understanding of the importance of co-constructing problems and questions.