Math

Mastering Elementary Math: The Power of MathReps and Math EduProtocols Pt. 4 Implementing MathReps

Image Admin1 Comment

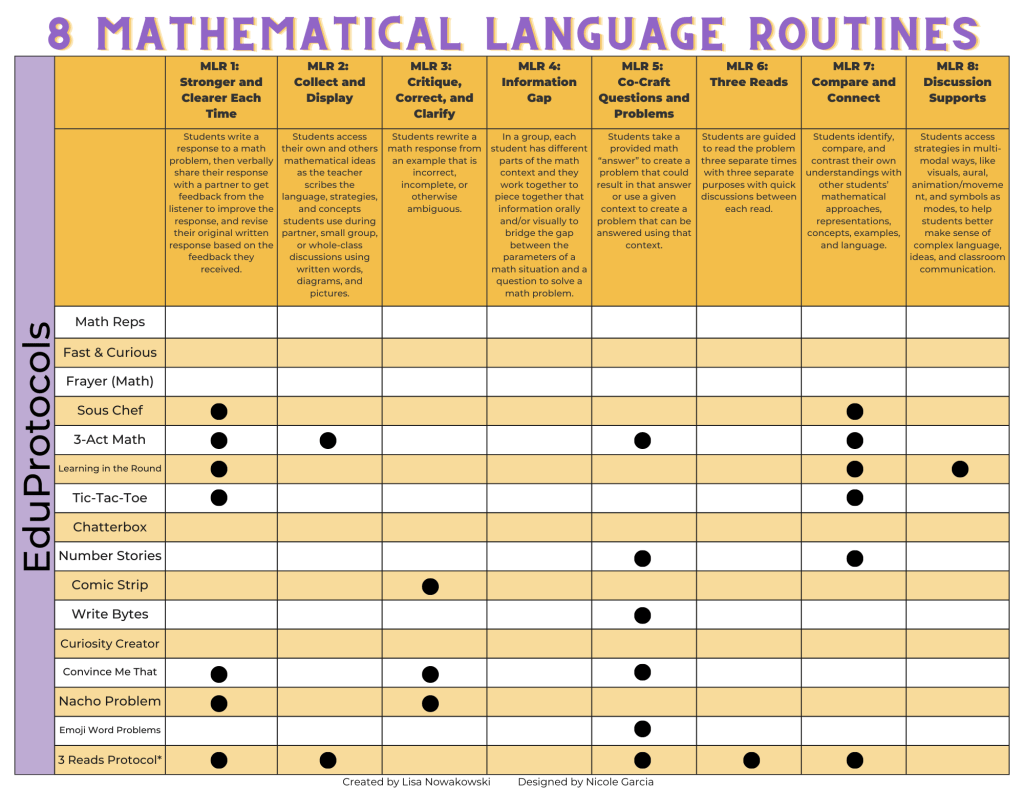
Getting Started with MathReps in Your Classroom

Here’s a suggested way to get started:

  1. Choose the Best Template:

    • Browse through the available MathRep templates and select the one that aligns with the specific skills your students need to practice.
    • Consider their proficiency level and the learning objectives you want to achieve.
  2. Introduce the Template and Work Through It Together:

    • Start by providing a brief explanation of the MathRep template to the class.
    • Guide your students through the process of completing the MathRep a few times together.
    • Break down the steps and demonstrate how to approach each section of the template.
    • Encourage students to ask questions and clarify any doubts they may have.
  3. Daily Practice for the First Week:

    • During the initial week, make MathReps a part of your daily math routine.
    • Assign the MathRep as a class activity and have students complete it with you.
    • Spend time reviewing and discussing the answers as a class, this emphasizes immediate feedback.
    • Use this opportunity to address misconceptions and reinforce problem-solving strategies.
  4. Independent Completion in Subsequent Weeks:

    • After the first week, assign MathReps for independent completion by each student.
    • Encourage students to work on MathReps at their own pace, within a given timeframe (following Parkinson’s Law).
    • Provide support to struggling students while encouraging higher achievers to challenge themselves.
    • Checking immediately with students provides crucial feedback.
  5. Weekly Assessment to Track Class Mastery:

    • Every Friday, use the MathRep template as a weekly assessment tool.
    • Collect and review completed MathReps to assess student progress and understanding.
    • This will help you identify areas where the class as a whole may need additional support or where mastery has been achieved.
  6. Transitioning to New Templates:

    • Once your class has demonstrated mastery of the current MathRep template, consider introducing a new template with new skills.
    • Gradually increase the complexity and challenge of the MathReps to keep students engaged and continually progressing.
  7. Review
    • Spend time reviewing previously used MathReps templates.
    • After students have become familiar, but not proficient, with a new template, spend a week reviewing a previous template.
    • This allows for the learning to ‘stick’.

Remember, adapt these steps as needed to suit the unique needs and learning environment of your classroom. MathReps can be a powerful tool for promoting mathematical proficiency and fostering student growth. Happy math practicing!

3 Reads Protocol

AdminLeave a comment

The “3 Reads Protocols” is a highly effective technique among the 8 Mathematical Language Routines. This strategy encourages a comprehensive understanding of word problems through a structured approach. In this activity, the problem is read three times, but it entails more than simple repetition. During the first read, the focus lies on comprehending the problem’s narrative. To aid in this process, teachers often conceal quantities and questions, enabling students to concentrate on comprehension rather than immediately diving into mathematical calculations. In the second read, teachers reveal the hidden quantities, redirecting students’ attention towards analyzing these values and their associated units, consequently deepening their grasp of the problem’s context. The final read diverges into two possible paths. If a question is provided, it is read aloud, and students formulate a strategic plan to tackle it. Alternatively, if no question is given, students are prompted to generate a list of inquiries themselves. Personally, I advocate for the latter approach, as it not only boosts student engagement but also fosters natural differentiation. In this scenario, students select a question from the generated list to solve. Remarkably, I have seldom witnessed students opting for an easy way out; rather, they frequently rise to the challenge by choosing appropriately challenging questions for themselves.

Today I was able to visit a 3rd-grade classroom in which the teacher was practicing this routine with their students. The teacher began by accessing the students’ prior knowledge about squirrels. The teacher then read the story (minus quantities) to the students. With partners, they discussed what the story was about. This can be hard for some students in the beginning. They know it’s math and naturally start looking for problems to solve. The students went through the steps and enjoyed themselves. After generating a list of questions, the group decided to answer the same question: How many acorns did each squirrel carry to get the pile of 24 acorns?

The struggle began as the teacher and I observed the students grappling with the task. We decided to give them some time to develop their own strategies before intervening. Many of them struggled to find a clear direction. Some counted the number of acorns squirrels can carry, reaching a total of 10. However, they seemed unsure about what to do next. Sensing the need for guidance, we asked the students to explain their thinking process. It was at that moment when a student appeared to have a promising approach. We asked him to elaborate on his reasoning. With a little clarification, he successfully explained that the black squirrel carried 15 acorns, while the gray squirrel carried 9 acorns. Surprisingly, the student didn’t mention the brown squirrel; technically, it carried 0 acorns. Another student followed suit and broke it down in a slightly different manner:

BrownBlackGray
253
253
121
Taking it one trip at a time

Doing it this way, the student was able to organize their thoughts and solve the problem in smaller chunks. At this point, we stopped the class to celebrate some early successes. With permission from the students, we shared each strategy pointing out how they are different yet correctly answered the question. By having the students explain their thoughts and showcasing some strategies this allowed struggling students to begin making sense of how to begin to tackle solving the problem. While some students still struggled others found similar strategies and were able to begin solving the problem.

The students agreed that this task was difficult, but fun. From our perspective, the students were engaged. As this was not the first time that students had experienced this, we can see small gains being made in the area of word problems. This is a protocol that the teacher plans to continue to use throughout the year.

8 Mathematical Language Routines

AdminLeave a comment

I have been on a journey to educate myself on the 8 Mathematical Language Routines (MLRs). While they were designed with Multilanguage Learners in mind, I find that they are just good teaching. So what are they?

  • Stronger & clearer each time
  • Collect & display
  • Clarify, critique, and correct
  • Information Gap
  • Co-craft questions
  • 3 Reads
  • Compare & Connect
  • Discussion Supports

So what does each one entail? Well, rather than sit and explain, I’d rather give you a resource that does a far better job breaking it down. It’s also one of my favorite resources.

Consortium on Reaching Excellence in Education

Part of my deep dive allowed me to align Math EduProtocols and these MLR’s. Doing this has my mind working on how to incorporate more MLR’s within Math EduProtocols.

With all this in mind, I have begun to curate some resources for teachers. I break down each MLR and give links to activities. It’s not a comprehensive list, so I will continue to add to it as I find more. If you have something that should be added to the document, let me know!

Nacho Problem

AdminLeave a comment

What’s a problem that’s not yours? Nacho Problem!

It’s that time of year, Test Prep time. Which makes me think about using EduProtocols for Test Prep. One great one that really promotes deeper thinking and understanding is Nacho Problem. This was created by Ligia Ayala-Rodriguez. It’s a fun way to do error analysis with your students. I have done this with students as young as 7.

One of the advantages is that you begin by telling the students the answer is wrong. This seemingly takes the pressure off. I like to have the students talk it out the first few times. I guide them along the way to help set the expectations. Just like in an ‘Analyze the Error’ on the test, students are expected to express their thoughts in writing. This can present an additional challenge if they haven’t exercised this skill. I’m not saying we should do this solely to prepare for the state test; the benefits of students being able to do this go far beyond that idea.

How to Get Started

As a class, they are presented with a Nacho Problem. We read and analyzed the problem together; starting with “What do you notice?” and “What do you wonder?” I explicitly tell them the answer is wrong and that we must find where I went wrong. I have found that looking at the question and working out the problem allows us to focus on the process (that the problem is asking us to solve) rather than the arduous task of finding a mistake. Once we work it out together, and later independently, students can then go back and compare their process with the original (wrong) process. It makes it more obvious where the original problem solver went wrong.

The written explanation can be the most difficult part. When I started doing problems like this, students would explain, in an addition problem, “I started in the ones and added 8+7. I left the 5 in the one’s place and regrouped the 1.” While technically that is true and we as teachers understand, that’s not showing an understanding. That is why practicing the structure of Claim, Evidence, and Reasoning (CER) is so important.

Claim: Ms. N. did not draw a quadrilateral.
Evidence: The student example with explanation.
Reasoning: Definition of a polygon and Ms. N’s error.

Finding Problems

One of the easiest ways to collect incorrect problems is from your class. Whether you use exit tickets or collect information from the day’s lesson, you have a plethora of options. When using student errors, it’s advisable to use a common mistake by many students. Done early, this can correct any misconceptions before they become habits. Ligia suggests using mathmistakes.org

Results

Teachers and students alike enjoy this math EduProtocol. Students find it ‘fun’ to find the mistakes. Teachers report that it takes little time to begin implementing in their classes. Doing this a few times a week can really improve understanding. Let’s face it, students LOVE to point out teachers’ mistakes.

If you use this, I would love to hear how it went. What changes did you make? How have your students improved with error analysis?

Free Bingo Cards

Image AdminLeave a comment

Recently I had a teacher ask me about some review games. Bingo is always a hit so I went on the search for a 3rd-grade Geometry Bingo game. Sadly, I couldn’t find what I wanted. Which then led to a search for Bingo card creators. I was not about to sit and recreate 25 Bingo cards. I like to use my time a bit more efficiently. And that’s when I found it! My Free Bingo Cards

This awesome sight creates simple Bingo Cards. They have several ready-to-go, broken down by categories. There is also the option to create your own. I opted to create my own. The process was simple. I plugged in all the words the students were to review. I then pressed one button for the program to create 30 unique Bingo cards. I did play around with it to see if I could insert images via copy/paste. No such luck. That was okay; I had a backup plan. The program also created a sheet for me to track which words were used and calling cards. I opted NOT to use the calling cards.

What did I use instead of the calling cards?

Instead of the calling cards I created a wheel on Wheel of Names. This was part of my backup plan: I used images. I could have also opted for the definitions, but I felt the images were more engaging and less repeating. This game was a big hit!

If you’re a 3rd-grade teacher and would like to play this here are the cards and here is the wheel.

If you’ve never used Wheel of Names before, you’re going to love it! There’s no need to guess where the spinner landed. The program tells you which one. Then you have the option to remove the selected item from the wheel to avoid mishaps.

Summer Presentations

Quote AdminLeave a comment

This summer, I will be presenting at two academies for EduProtocols. My sessions will have a math emphasis; shocking, I know. So this past week when I was asked to come up with titles and descriptions, I struggled. I wasn’t feeling it. Luckily, a friend called before I could toil for too long. I relayed to her my lack of motivation at the time, and she came up with some catchy titles.

  • 🍸The Mixology of MathReps – MathReps
  • Wheel Of Word Problems – Word Problems with Random Emoji
  • Playing with Parts – 8 p*ARTS meets word problems
  • 🌶️🌶️ Spicey Solutions to a Bland Curriculum – Nacho Problem
  • 👩🏽‍🍳Chef’s Kiss – Sous Chef
  • Frayas for Ya Playas – Frayer and, honestly, my favorite title
  • 🦹🏻‍♂️Math is a Villain: Comic Strip Math

Then it was time to get started on the descriptions. This is where I got inspired. I doubled down on the titles and all descriptions fit that theme. I mean, check out this description for Comic Strip Math:

In a world full of villains, the fine citizens of Mathemagicalville are up against the most evil, vile, sinister one around. Master of Dark is relentless in the pursuit of conquering the city. It is up to you, the superhero, to prove Master of Dark wrong and find the errors that were made. You create the comic, find errors, explain processes, and become the hero the city needs.

Yes, Mathemagicalville is a mouthful, but the names I wanted were all taken, and so I had to become creative. When I was creating this description, I felt that I had to be very careful with my wording. The character ‘Master of Dark’ was created by my 5th-grade class at the time, around 2019. The character was created to be gender-neutral. However, in today’s political climate, with hundreds of anti-trans laws being introduced throughout the country, I want to be sensitive to this. In 2019, the intent was to NOT represent one group as ‘evil’ or ‘bad’ but to keep the focus on math while empowering ALL the students in my classroom. The empowerment came from not having the gender stereotypes that boys are better at math than girls, and by taking the gender out of character seemed like a good solution at the time. However, as I began writing the description, I tried avoiding any pronouns. I don’t want to put a negative focus on any group.

I may be overthinking all this, and I may not be. However, in cases like this, I would rather err on the side of caution. So what do you think? Am I overthinking this? Does this character need to be revisited? Do I simply avoid using any pronouns as it’s not critical to the purpose of thinking critically about math? I would love to hear from everyone, especially those in marginalized communities.

Okay, that took a serious turn. NOW if you’d like to join me in Laguna Beach or Notre Dame this summer, here’s more information. I can’t guarantee that all seven sessions will be presented at both, but I can say that MathReps and Comic Strip Math will be presented at both – if I have a say.

Extra Practice

Image AdminLeave a comment

This year I began using ‘Classroom Economy’. The students have jobs, earn money, and rent or buy their desks. Students have several opportunities to earn extra money. This is important because their monthly paychecks are less than their rent ($1000).

One way they can earn extra money is to solve math problems. I post two problems for anyone in the class to solve. I will only take the first correct answer. One is generally more difficult than the other thus allowing students to challenge themselves. The harder problem will earn them $50 while the easier one will earn them $20.

I was able to snap this photo of a student, who NEVER passes up the opportunity to make extra money, practicing the skills that she has learned. Added bonus, we leave the process a student takes on the board for all to see and learn from.

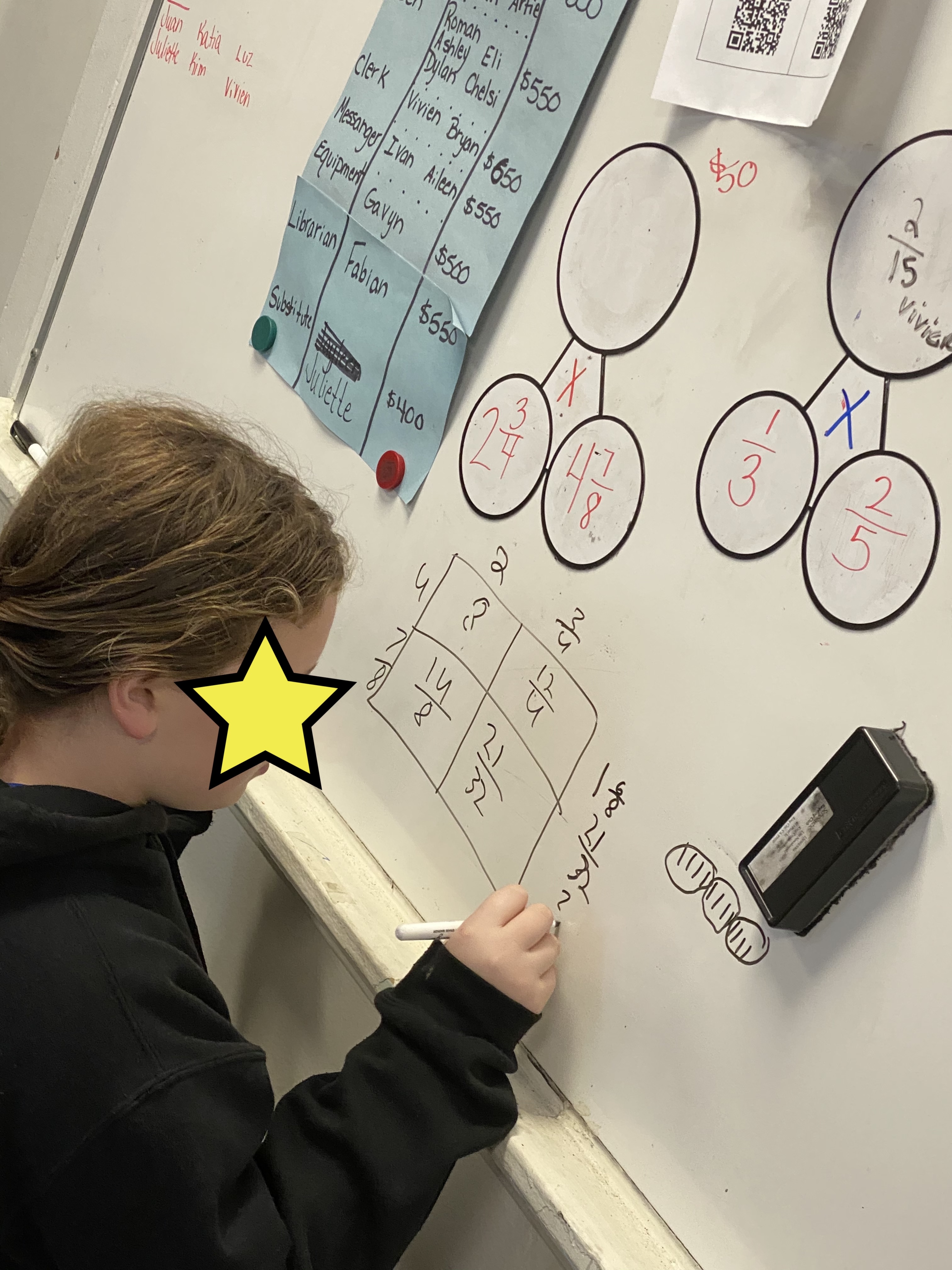
Math Practice

 

92%, Say What?

Image AdminLeave a comment

92%So what’s the big deal with 92%? A lot when it comes to having 3 weeks off and the likelihood that none of my students practiced their multiplication facts.

Monday was our first day back after winter break. As we do every day, we practiced our math facts using the Fast & Curious Eduprotocol. I had an anticipated drop from our usual 96% – 98%. I predicted, to myself,  it would drop to around 89%.  I wasn’t too concerned as I knew that they could easily get it back up to our normal within a week.

Well, to my surprise, my class scored 92%. Seriously, I was happily surprised that they really didn’t lose as much as I had feared. YES! The continuous rep practice has worked. The facts are sticking.

I was so giddy, I needed to write this quick post to celebrate the success my class is finding. I was sold before, but now I’m a believer for life!

Math Facts with Fast & Curious

Image Admin7 Comments

Resistant

I will admit, I was reluctant to use any sort of ‘timed tests’ for math in my classroom. The research does not support it. However, my students were sorely lacking in their multiplication skills, a skill they should have mastered by now. At conferences in September, I spoke with each parent about the need to practice at home and easy ways they could help their child. After a month, there was little improvement. THEN, I had a conversation with Jon Corippo.

Jon suggested I use the Fast & Curious Eduprotocol with math facts. I knew he had convinced Cori Orlando to try this with her 3rd graders previously. She balked at first then became a believer. I still held out. He gave me the same spiel he gave Cori. I begrudgingly tried it. It felt too much like timed tests. At first, the kids loved it; it was something new. But then, they kept asking for it day after day. This lasted a while. Several months later, they STILL beg for it.

Does It Really Work?

Simply put, yes. The data speaks for itself. In the beginning, we were averaging around 56% as a class. That’s 56% correct on a 10 – 20 multiplication question quiz. As a class, we could only score 56% on a quiz. And some quizzes we were a bit lower (48%). YIKES! Within two months, as a class, we score between 96% and 98% no matter the quiz I give them. That doesn’t mean that I still don’t have kiddos who are struggling, I do. I still have kiddos who take an incredibly long period of time to complete it. Some day, I have to end the quiz before everyone can finish. But let’s face it, going from 56% – 96% is a drastic difference. I’ll take it!

pexels-photo-1329296.jpeg
Photo by Magda Ehlers on Pexels.com

My Process

I use Quizizz, a computerized gaming review system. It’s a mouthful but if you’re familiar with Kahoot, it’s very similar. I choose a multiplication quiz. No need to make your own, just do a search and you’ll find one. Set up the quiz in classic mode and have the students sign in. On day 1, we take the quiz twice. The first time is cold, we write down our score (Quizizz is great that it’ll average your class score for you), review the questions, then take it again. We keep our first score then we record our second score to see how much we’ve improved. For the rest of the week, we take the same quiz. If our score goes up, which it should, we erase the last high score and replace it with the newest score. We repeat this process with a different quiz the following week.

Because students can consistently score in the 90% range on the first go-around no matter the quiz, I only do the quiz once on Mondays. I have some added bonuses you can read about.

Cheating

I have teachers ask if students cheat: help each other, start the quiz over again, tell another student the answer. The answer is yes. But I don’t care. The kids who are getting the answers are clicking the correct answer and reinforcing it. Those that take it again are practicing twice as much as everyone else. It’s really a win-win.

I’m a Believer

Based on all that I have seen in my classroom, I am now a believer in this protocol. The kids still love it months later. The information is transferring. The data doesn’t lie. Even if you’re still reluctant, give it a try. I did and so did Cori!

Tic Tac Toe Math

Image AdminLeave a comment

I have been on a creative streak lately. I LOVE #EduProtocols by Marlena Hebern and Jon Corippo. I LOVE #MathReps which were inspired by Jon Corippo’s 8 p*ARTS of Speech (read the full story). As a result, I have been working on Math EduProtocols. My latest one, that is ready to share with the world and receive feedback, is Tic Tac Toe Math.

Tic Tac Toe Math (1) This is a sample I created for my class. My intent was to review some basic math concepts while having fun. The rules are simple:

Each player writes their name and chooses either X or O.

  1. Player 1 chooses a square to complete. BOTH Player 1 and Player 2 independently work out the problem in the chosen square.  If Player 1 is correct, Player 1 gets the square and circles their symbol (X or O)
  2. IF Player 1 is incorrect, Player 2 has a chance to ‘steal’ the square. Player 2 MUST complete the problem correctly AND explain where Player 1 was incorrect.
  3. Player 2 chooses a square, even if they stole Player 1’s square. BOTH players must work independently to solve the problem. If Player 2 is correct, Player 2 gets the square. If Player 2 is incorrect, Player 1 has a chance to ‘steal’ the square. Player 1 MUST complete the problem correctly AND explain where Player 2 was incorrect.
  4. This continues until someone wins or all squares have been completed.

I tested it out on my students. They liked it and had some good feedback. Some wanted ALL algorithms. Some wanted harder problems. This was a fair statement as I purposefully chose easier problems. I wanted to hook them before going all in. Two students worked on the middle square together and decided that they both claimed it; that worked for me. Overall, it was something that they all enjoyed.

The set up of the problems was purposeful. The four corners are meant to be easier problems (DOK 1). This allows all students success. Those that are between the four corners are meant to be a bit harder. Finally, the center square is to be the hardest. A challenge problem. A player can still win without choosing the challenge problem. I did like the modification my students came up with for that middle square. It takes the pressure off one particular player and allows for collaboration, problem-solving, and communication between players in a friendly manner.

I have created a template with directions and the above sample. Feel free to copy and create your own. I would love to hear how you are using it and how your students feel about it. What modifications have you made? Please share!