Eduprotocols

Engaging Students with Parts of Speech EduProtocols

AdminLeave a comment

In my last blog post, I shared a story about coaching alongside a third-grade team that includes one of my former 5th-grade students.

Beyond our fun Skippyjon Jones read-aloud moment, my primary focus with this team has been elevating student writing. To help students become stronger, more intentional writers, the team wanted to introduce a classic EduProtocol: Parts of Speech.

To kick things off, I modeled demo lessons in each of their classrooms. By last week, the teachers were ready to take the reins and lead the protocol independently.

From Nervous Energy to Classroom Excitement

While heading over to visit my former student’s classroom, I ran into another third-grade team member. She was equal parts excited and nervous, mentioning she was planning to run her first solo Parts of Speech lesson later that afternoon. I promised to stop by.

When I popped into her room, the magic was already happening.

She was projecting a visual prompt on the display (an image of a sleeping kitten cozy in a blanket) alongside a collaborative word bank grid. The students were completely hooked and actively engaged.

How She Structured the Lesson

Her instructional execution was a textbook example of scaffolded support:

  1. Whole-Group Brainstorming: Together as a class, they generated targeted word banks across four columns based on the image: nouns, adjectives, verbs, adverbs.
  2. Guided Modeling (Sentence #1): She walked the class through constructing the first sentence together on the board, demonstrating how to pull words directly from their generated lists into a coherent, grammatically correct thought.
  3. Independent Application (Sentences #2 & #3): Once the structure was clear, she released the students to craft their own unique sentences for slots two and three, with the requirement that they pull from their shared vocabulary bank and use the parts of speech correctly.

Teacher Insights and Next Steps with Snorkl

The third-grade team is already noticing positive gains. Students are identifying parts of speech much faster, though the team noted that distinguishing between adjectives and adverbs still requires ongoing practice. Because EduProtocols rely on repetition and familiar frameworks, they will continue to refine these concepts in upcoming sessions.

Their next iteration? Tech integration via Snorkl.

The team plans to have students dictate their finished sentences into Snorkl, combining oral language practice, immediate feedback, and sentence construction into one seamless routine.

Seeing teachers move from watching a demo lesson to confidently leading high-engagement writing protocols in their own rooms is what coaching is all about. I’ll keep you posted on how their Snorkl dictation integration goes!

How do you help your students bridge the gap between isolated grammar practice and active sentence writing? Let me know in the comments below!

Sustainable Daily Math Routines: Engaging Feedback Strategies

AdminLeave a comment

When teachers first see MathReps in action, their biggest question isn’t usually why it works; it’s how to keep it going day after day.

How do you run a daily math routine without burying yourself in a mountain of grading every evening? The secret to sustainability lies in closing the feedback loop immediately during class time. This is true for all EduProtocols.

In John Hattie’s extensive Visible Learning research, feedback ranks among the highest-leverage instructional practices with an effect size between 0.70 and 0.75. Considering Hattie’s 0.40 “hinge point” represents a standard year of academic growth, actionable feedback nearly doubles the rate of student learning. But that research assumes feedback happens when it matters most: in the moment of learning, not two days later on a returned worksheet.

Whether you operate in a high-tech 1:1 digital environment, prefer the simplicity of paper-and-pencil, or use a hybrid approach, MathReps is designed to deliver high-impact feedback without burning you out.

Here are four ways to make MathReps sustainable in your daily routine:

1. The Low-Tech, Low-Stakes Standard: Dry-Erase Sleeves

One of my personal favorite ways to run MathReps is using clear plastic sheet protectors or menu sleeves with dry-erase markers. The fine-tip dry-erase markers work the best.

Slide a printed MathRep template into the sleeve, and students are ready to work. This approach offers two major advantages:

  • Low-Threat Environment: If a student makes a mistake, a quick swipe of an eraser fixes it instantly. The low risk encourages students to try strategies they might hesitate to write down on paper.
  • Real-Time Clipboard Feedback: Because students complete the work in 5 to 10 minutes, you can roam the room with a dry-erase marker, providing that high-effect-size feedback in real time. Misconceptions are addressed on the spot, and mastery is checked off live.

When the time is up, students erase their boards, leaving the template pristine and ready for tomorrow morning; no copying required.

Bonus: place an example on the opposite side of the blank MathRep for students to reference.

2. Paper & Pencil Checks

If you prefer paper, sustainability comes down to shifting when and where grading happens. Instead of collecting papers to grade at your desk, make feedback active.

As students work through their MathRep, walk the room. Spot-check key concepts, stamp completed work, and address misconceptions right at the student’s desk. By the time the 10-minute timer rings, 90% of your feedback has already been delivered face-to-face, eliminating the need to take papers home.

3. Leveraging Tech for Instant Feedback: Snorkl

Student Snorkl screen showing MathReps

If you want to streamline your digital workflow and enhance student explanations, Snorkl is a powerful partner tool for MathReps.

Snorkl provides immediate, automated feedback to students as they record and explain their thinking, hitting Hattie’s feedback sweet spot automatically. Even better, pre-built MathReps templates for Grades K through 5 are already built into the Snorkl library and ready to assign.

The Hybrid Wipebook Workflow: You don’t have to choose strictly between physical and digital. Many teachers have students complete their MathRep on a non-permanent surface, such as a Wipebook (or dry-erase sleeve), take a quick photo of their work, and upload it to Snorkl. Students then record a brief audio explanation of their reasoning over the image. Snorkl provides immediate feedback on their explanation, giving students double the processing power without adding to your evening workload.

4. Small-Group Targeted Interventions (Tier 2)

Sustainability also means using your instructional time efficiently. While the majority of the class works independently or in partners on their daily MathRep, you (or an instructional aide) can pull a small group of students who need targeted support.

Using a foundational or modified MathRep template, you can address specific skill gaps in a small-group setting. Because the format matches what the rest of the class is doing, students receive targeted, high-dosage feedback without feeling isolated or singled out.

Work Smarter, Not Harder

A daily routine is only as good as its longevity. By leveraging immediate feedback – whether through a dry-erase marker while roaming the room or an audio-recording tool like Snorkl – you tap into one of the most powerful learning effects in educational research while keeping your time manageable.

How do you run MathReps in your classroom? Are you team dry-erase sleeve, team paper, or team Snorkl? Let me know in the comments below!

Maximizing Tier 1 Math Instruction with MathReps

AdminLeave a comment

Before we dive into how MathReps fits into daily classroom instruction, let’s review what Tier 1 actually is.

In a Multi-Tiered System of Supports (MTSS) framework, Tier 1 is the core, universal instruction that all students receive. Often referred to as “best first instruction,” the goal of Tier 1 is to provide high-quality, grade-level learning that meets the needs of roughly 80–85% of students without requiring outside intervention.

The goal of Tier 1 is simple: build a solid foundation early, so we avoid creating learning gaps. As every educator knows, when a math gap is left unaddressed in the early years, it grows exponentially wider as a student progresses through school.

This is precisely where MathReps shines. MathReps isn’t a “fun extra” or a filler activity; it is a powerful engine for Tier 1 core instruction.

The Core Characteristics of Effective Tier 1 Instruction

To understand why MathReps works so well at the Tier 1 level, we have to look at what makes core instruction effective in the first place:

  • Universal Access: Every student engages directly with grade-level standards and core mathematical concepts, rather than being isolated into low-level remediation.
  • Low Cognitive Load: Instructional frameworks and routines are structured predictably so students spend their mental energy wrestling with mathematical concepts, not deciphering complicated directions.
  • Spaced Retrieval & Mixed Practice: Learning relies on continuous, spaced exposure across time to build automaticity, fluency, and long-term retention.
  • Real-Time Formative Assessment: Daily insights allow teachers to check for understanding on the spot, adjusting instruction in real time rather than waiting for an end-of-unit test.

How MathReps Powers Your Tier 1 Math Block

Here is specifically how a daily 10-minute MathReps routine fulfills the promise of Tier 1 instruction:

1. Low Floor, High Ceiling Accessibility

Tier 1 instruction must serve learners at various entry points. Because MathReps utilize consistent visual models (such as ten-frames, area models, place value charts, and number lines), every student can access the prompt at their current level of understanding. At the same time, open-ended quadrants provide natural depth and extension for advanced learners.

2. Spaced Retrieval Over Isolation

Traditional math curricula often present concepts in isolated silos; teaching division for three weeks in October, moving on, and never revisiting them until the end-of-year exam. MathReps embeds spaced retrieval into daily practice. By continuously cycling through core standards across the entire school year, students build durable retention and see connections across mathematical domains.

3. Reduced Cognitive Load Through Familiarity

When the layout of a MathRep remains consistent over a 6-to-8-week cycle, students don’t waste working memory trying to figure out how to do the worksheet. Because the format is predictable, 100% of their cognitive capacity is freed up to focus on the actual math.

4. Immediate, Actionable Formative Data

A core goal of Tier 1 is catching misconceptions before they turn into gaps requiring Tier 2 or 3 intervention. During a quick 5- to 10-minute MathReps session, you can scan the room or review digital submissions (like Snorkl) in real time. You instantly know who needs a 2-minute check-in, what needs whole-class clarifying, and who is ready for an extension.

5. Seamless Warm-Up Integration

As an EduProtocol-aligned routine, MathReps serves as the ultimate Tier 1 practice. It sets a predictable, success-oriented tone for the math block, builds confidence through daily wins, and normalizes a classroom culture grounded in mathematical discourse and reasoning.

Teach with Confidence

Because MathReps aligns directly with the research behind effective Tier 1 instruction, you can feel 100% confident bringing it into your classroom every single day.

If an administrator ever walks into your room and questions what you are doing (as has happened to me) or asks for the pedagogy behind the routine, you have a clear, research-backed answer: MathReps is high-leverage, low-cognitive-load Tier 1 instruction designed to catch gaps before they start.

How has MathReps helped your Tier 1 instruction?

Enhance Math Skills with the 8 Mathematical Language Routines

AdminLeave a comment

As we kick off a new school year, one of our primary district priorities is diving deep into the 2023 California Math Framework. While curriculum frameworks can sometimes feel dense or disconnected from the daily realities of the classroom, there is one aspect of this framework I genuinely love: its deep grounding in the 8 Mathematical Language Routines (MLRs).

Back in 2023, while sitting with my dad in his hospital room, I wrote an extensive series breaking down these routines. (You can explore the full breakdown and access a comprehensive collection of explanations, examples, and resources in this resource document).

If you are familiar with the 2013 California Math Framework, it focused heavily on vertical content progressions, showing how a concept like addition moves from number paths in Kindergarten to visual area models in 2nd grade, ultimately culminating in the standard algorithm by 4th grade. The 2023 framework doesn’t replace that progression; it elevates it by embedding specific routines designed to build language, conceptual fluency, and student discourse.

While implementing all eight routines at once can feel overwhelming, you don’t need to do everything on Day 1. Here is a close look at my top two go-to routines, plus a high-impact bonus routine, to get you started.

1. Routine #6: The 3 Reads Protocol (Plus the Essential “Plan” Step)

Word problems are notoriously difficult for students because their brains are forced to work double-duty. First, they must execute ELA reading comprehension skills to parse the text; then, they must activate their mathematical processing to execute the computation. For multilingual learners or students with reading disabilities, this cognitive load can be paralyzing (I speak from experience).

The 3 Reads Protocol deconstructs the word problem into manageable, bite-sized cognitive steps:

  • Read 1 (Context): Read the problem without focusing on numbers. The sole goal is to understand the situation and visualize what is happening. Drawing out the scene can help students visualize it.
  • Read 2 (Quantities & Relationships): Read the problem a second time to identify the numbers, units, and how those quantities relate to one another.
  • Read 3 (The Task): Read a third time to isolate the specific question or mathematical task.

My Practitioner Twist: Adding “The Plan” Typically, I see student thinking break down right after Step 3. Students know the context, the numbers, and the question, but they freeze when deciding what to do with that information. That is why I always add a fourth step: Designing a Plan/Model. We analyze how we will answer the question, often by drawing out an area model, bar model, or diagram. Running this protocol several times a week as a whole group removes the mystery from word problems and builds durable problem-solving habits.

2. Routine #3: Clarify, Critique, and Correct

How often have we told a student to “go check your work,” only for them to glance at their paper for two seconds and say, “Yup, looks good”? Telling students to check their work without teaching them how to critique math is ineffective.

Routine #3 teaches students to analyze mathematical reasoning critically; first in others, and ultimately in themselves. My favorite way to execute this is through the EduProtocol Nacho Problem.

You present a math problem containing a common conceptual error. Students must locate the mistake, correct the procedure, and, most importantly, write about it using a C.E.R. (Claim, Evidence, Reasoning) structure. When students have to justify why an error occurred in writing, their understanding shifts from surface-level recall to deep conceptual mastery.

3. The Bonus Routine: Co-Craft Questions (Routine #5 / 3-Act Math)

This routine is an incredible tool for student engagement and organic differentiation. You present students with a rich scenario or visual context without providing a final question. Students are then tasked with co-crafting mathematical questions that could be answered using the provided information.

The beauty of this routine is that students naturally differentiate the math themselves. You will see students generate “mild, medium, and spicy” questions. When given the choice, the vast majority of students will naturally challenge themselves with a more complex question than the one a teacher might have assigned them.

Classroom Management Pro-Tip: What about the student who intentionally chooses the easiest possible question? Let them! They will finish it in 30 seconds. When they do, simply say, “Great job. Now choose one of the spicy questions to tackle.” If it becomes a habit, offer a structured choice: “You can choose Question B or Question C today.” They retain autonomy, but the floor of rigor is raised.

Which Routine Will You Try First?

No matter which Mathematical Language Routine you choose to introduce to your math block this semester, you are giving your students the tools to move beyond procedural compliance and into true conceptual understanding.

Which of these routines are you going to test out with your students first? Let me know in the comments!

Launching MathReps

AdminLeave a comment

Getting MathReps started at the beginning of the school year doesn’t need to be overwhelming. In fact, when structured intentionally, it is one of the easiest ways to transform your math culture from day one.

Too often, math is viewed by students as a hurdle, a mucky, frustrating chore that has somehow become socially acceptable to trash-talk. MathReps flips that dynamic by prioritizing immediate success and predictable routine over high-stakes execution.

Here is how to soft-launch MathReps in your classroom, build student confidence, and streamline your management from week one.

1. Soft Launch with a 2-Week Prerequisite Cycle

Before jumping into your core 6-week grade-level cycle, run a 2-week prerequisite cycle.

During these first two weeks, select a MathRep built entirely on skills from the previous grade level. When students already know the math, they aren’t fighting two battles at once. They can focus 100% on learning your expectations, understanding the layouts, and mastering the daily pacing. Starting with familiar material builds immediate self-efficacy; students feel successful right out of the gate, and you establish the routine smoothly. It’s a win for everyone.

2. The 6-Week Implementation Timeline

Once your 2-week prerequisite launch is complete, you move into your first full 6-week grade-level cycle. Expect the daily timeline to shift rapidly during Week 1 of any new Rep:

  • Week 1 (Building the New Rep):
    • Day 1: Expect this to take up to 45 minutes. You are walking through every section together, establishing vocabulary, and setting expectations.
    • Days 2–4: Pacing drops fast. As students grasp the format, time will shrink from 30 minutes down to 12–15 minutes or less by Day 4.
    • Day 5: Use this rep as a baseline assessment to track growth.
  • Weeks 2–6 (Independent Execution & Immediate Feedback): Set daily time limits (10–12 minutes), have students complete their reps, and check them immediately. The time limits are based on Parkinson’s Law. Give them enough time to finish the task, whether you break it into chunks or do the whole MathRep at once. Use Friday as your weekly progress check.

3. Practical Setup & Differentiation Pro-Tips

  • Low-Stakes Management with Plastic Sleeves: Slide a blank MathRep into a dry-erase plastic sleeve. This saves thousands of copies over the year, but more importantly, it lowers student anxiety; erasing with a marker is psychologically much easier for a struggling student than erasing paper and tearing the page. Bonus: Slide a completed example or anchor chart on the back side of the sleeve so students have an instant reference tool.
  • Anchor in Interactive Notebooks: Complete one full MathRep as a whole group early in the term and have students glue it directly into their interactive notebooks as a reference page for the rest of the year.
  • Differentiate with Choice Boards (The 2-Week Mastery Rule): If a student demonstrates proficiency on a specific MathRep two Fridays in a row, pivot them off daily repetitions and onto a Choice Board for deeper, practical application. To maintain Choice Board status, students must continue showing mastery on the Friday assessments (or through a teacher checkpoint built into the Choice Board itself). This keeps proficient students challenged while freeing you up to target support where it’s needed most.
  • Streamline Feedback with EdTech: If checking Friday assessments feels daunting, leverage tools like Snorkl. It gives students immediate, diagnostic feedback, limits response attempts to keep them focused, and provides you with instant analytics without drowning in paper. (If you teach K–5, pre-built MathReps are already loaded in Snorkl and ready to assign).
  • Elevate Learning through Metacognition: Practice without reflection is just compliance. Have students complete a weekly reflection log analyzing what went well, where they struggled, and how their conceptual understanding shifted over the five days.

What strategies or management hacks have you used that aren’t listed here for a smooth start with MathReps in your math class?

Reflections on Year 31: Growth, Gratitude, and Navigating the Unknown

AdminLeave a comment

Reflecting on a school year is always a delicate balance of celebrating deep classroom triumphs while navigating the inevitable winds of systemic change. This year marked my 31st year in education. If three decades in the classroom and in coaching roles have taught me anything, it is that while our daily tasks may shift, the core mission of supporting authentic student and teacher growth remains entirely unchanged. Looking back at the full landscape of the months behind me, I can confidently say it was a year filled with personal and professional success, driven by educators and students willing to take risks and try something new.

The best moments of my year took place directly inside classrooms, where I had the privilege of watching brilliant teaching across several grade levels. In Kindergarten, students were mastering foundational coding using Bee-Bots, while up in 5th grade, classrooms were diving into collaborative critical thinking through the Cyber Sandwich EduProtocol. As a Tech TOSA and instructional coach, my favorite days involved partnering with teachers to blend meaningful technology with powerful pedagogical frameworks. In one room, we paired MathReps with Wipebooks and Snorkl to make mathematical thinking visible and dynamic. In a 2nd-grade classroom, the students proved to be absolute rockstars in independent reading comprehension, leveraging Snorkl to capture their responses before seamlessly transitioning to choice boards to further explore topics independently.

Perhaps the most profound professional joy this year came from an instructional coaching cycle focused on student discourse with a 1st-grade teacher. By implementing just a few precise, intentional shifts, this teacher increased student-led discussion by an incredible 62% in a short six-to-eight-week period (I think it was six weeks, but I tell ya, it’s been a year). The transformation came down to a few key pedagogical changes: intentionally giving the students dedicated time to share ideas with one another before speaking to the whole group, and introducing structured sentence frames to support their developing language skills. The most rewarding part of this growth was that these targeted design shifts ultimately saved the teacher a great deal of time and energy, proving that shifting the cognitive load to our youngest learners is a win for everyone.

Beyond individual classrooms, our district has continued its steady journey into standards-based learning in mathematics. Refining our proficiency scales has brought massive clarity to our school sites. Through this ongoing work, our teachers now possess a much deeper understanding of the standards and a clearer picture of exactly what is expected of our students to build true conceptual understanding. Which led to many discussions as we evaluated which Math curriculums to pilot next year. On a professional level, I also adjusted to a new supervisor this year: our Director of Curriculum and Instruction. Navigating a change in leadership always requires a period of mutual adaptation.

Of course, a year rarely goes by without some friction, and it certainly wasn’t all smooth sailing. At the district level, it was a genuinely rough year marked by internal site issues that caused considerable unrest, leading to some contentious board meetings. Compounding this unrest was the sudden announcement that our high school district will unify with us within the next three to five years due to the desired unification of a neighboring town’s elementary district. (NOTE: our high school district is in charge of our town’s high school and the neighboring town’s). It is a massive undertaking, and the reality is that we simply are not ready and currently have no viable plan in place. To add to the complexity, our superintendent decided to retire this past spring. Because the announcement dropped so late in the school year, it left very little time for a thorough, comprehensive search for a new leader who is ready to take on both our internal site challenges and a looming district unification. As of today, the district has been in negotiations with one candidate, but that is as far as it has gone (as far as I know), leaving us entering the summer with real uncertainty about who will be leading our district forward.

Looking back at the year, it was a journey filled with intense ups and downs. Unfortunately, there were far more bumpy patches than smooth ones this year. While our absolute focus should always remain firmly on our students, the honest truth is that maintaining that focus can be incredibly difficult when there is so much systemic upheaval going on all around us. Some school sites felt this weight much more than others. It was a heavy, exhausting year for many.

Looking ahead to the upcoming school year, we have a major math pilot in place to evaluate two distinct approaches to conceptual understanding. We will be taking a deep look at Innovamat’s Thinking Math alongside Savvas’ EnVision, and I am eager to see how our teachers and students interact with these resources as we continue to refine our standards-based instruction.

Here’s to closing out year 31and to stepping into year 32 (YIKES). Seriously, though, how did so many years already pass by? It truly feels like I just started teaching ten years ago. Wherever the road leads and whoever steps in to lead our district, my hope is simply that this next year brings a little more stability and a lot more smooth patches for our district.

The Power of the “Number Menu” in MathReps

Admin1 Comment

We’ve all been there. It’s your math block, and you’re asking students to run a Place Value MathRep. You need a number to work with. You could ask a student for a random number, and depending on your class, that could be dangerous. 6-7 anyone?

But what if we gave them a Menu instead?

The Number Menu is a simple, low-prep strategy to turn a standard MathRep into a high-interest, culturally relevant experience. By providing a curated list of 5–10 real-world numbers, you give students agency, choice, and a reason to care.

Why it Works

  • Natural Differentiation: Include a “Mild, Medium, and Spicy” option. A teacher can put a 2-digit, 4-digit, and 7-digit number on the same menu, allowing students to self-select their challenge level.
  • Connection: It bridges the gap between the classroom and the community.

Build Your Menu: 5 Categories to Get Started

You don’t need to reinvent the wheel every day. Pick a few categories, update the numbers once a week, and post them in a dedicated corner of your whiteboard.

1. The “Home Base” (Local Landmarks)

Perfect for place value, rounding, and measurement.

  • The School’s Address: Use the street number of your building or a famous local landmark (local library, coffee shop, or grocery store).
  • Local Elevation: What is the altitude of your town? A nearby town? (Great for comparing numbers!) You could even do the population!
  • The Distance: How many miles is it from your classroom to the nearest State Capital? Or city hall?

2. The “Scoreboard” (Sports Stats)

Sports are a universal language for engagement.

  • The Box Score: Points scored, total rushing yards, or the attendance at last night’s local or national game.
  • Jersey Math: Use the numbers of local high school stars or professional athletes. This is perfect for the 4 operations with double-digit numbers.
  • Pro-Tip: Don’t be afraid to be a “homer”! Why not use at least one Detroit Lions stat on the menu? What a great way to engage in math! Not a Lions fan? (Why not? – don’t answer that), Use a favorite team of yours or your students.

3. The “Main Street” (Community Math)

Connecting math to the economy that students see every day.

  • Price Points: The current cost of a gallon of gas or a local favorite “Happy Meal.”
  • Elapsed Time: If the local library opens at 10:00 AM and closes at 6:00 PM, how many minutes is it open?
  • Historical Age: The year your town was founded vs. the current year.

4. The “Trend” Report (Pop Culture & Digital)

Meeting students where they live—online.

  • The Viral Count: Use the view count (in the millions!) of a trending (and school-appropriate) video or song.
  • Gaming Stats: The current “active player” count for games like Minecraft.
  • The Countdown: How many days/hours until the next big movie release? Or a local event like the Salinas Valley Fair?

5. The “Wildcard” (Nature & Science)

For the kids who love the “did you know” facts. I love this idea. So many random

  • The Weather: Today’s high and low temperatures (perfect for introducing negative numbers).
  • Animal Facts: The weight of a local species vs. an exotic one (e.g., a Black Bear vs. a Blue Whale).

Keep it Simple

The goal of MathReps is to keep the routine stable so the thinking can be deep. You don’t need a fancy tech integration for this. A simple “Weekly High Five” list on the board is all it takes to transform a routine repetition into a meaningful conversation.

When you bring the world into your MathReps, you aren’t just teaching place value—you’re showing students that math is happening all around them.

What numbers or topics are on your menu this week?

Poster Template

The Spring Lifeline: Zero-Prep, High-Impact Math Review

Admin2 Comments

It’s the end of April. If you’re like most teachers, you’re spent. Your students are spent. But the learning doesn’t stop just because the calendar flipped.

How do we keep the “polish” on our math skills without adding more prep to an already overflowing plate?

The “Assign and Go” Solution

I am thrilled to share that MathReps are live and pre-made inside the Snorkl library. No more standing at the copier. No more hunting for the right PDF. You can quite literally “Assign and Go.” Whether you need to sharpen the 4 operations or dive deep into fraction models, the heavy lifting is already done for you. And what a relief that is!

Why This is a Game-Changer Right Now:

  1. Zero Prep: Navigate to the Snorkl Library, click “EduProtocols,” and select “MathReps.” Everything from Kinder to 4th Grade (with 5th Grade coming soon!) is ready to push out to your students instantly.
  2. The AI Co-Teacher: At this point in the year, you don’t have the bandwidth to listen to 30 individual explanations. Snorkl’s AI does it for you. It listens to the student’s logic, catches the “Instructional Debt” (like that hidden skip-counting), and provides immediate feedback. Although you may have to remind the students to review the feedback, I’m finding that in some younger grades.
  3. Consistency Over Novelty: Since these are based on the MathReps your students already know, you aren’t teaching a new tool; you’re just using a better engine to run the routine.

How to Find Them:

It couldn’t be easier.

  • Log into Snorkl.
  • Navigate to the Library.
  • Look for the EduProtocols section.
  • Select MathReps.

A Quick Update for 5th Grade

I know my 5th-grade teachers are waiting. I’m currently getting those frames ready for you! Stay tuned; they’ll be live in the library soon to help you finish the year strong.

The Bottom Line: You don’t have to choose between your sanity and your students’ growth. Let Snorkl handle the prep and the feedback so you can focus on being the human connection your students need as we close out the year.

15-Day Routine for Math Test Confidence

AdminLeave a comment

In the sports world, athletes don’t spend the week before a championship learning new plays. They spend it “polishing”, perfecting their form, sharpening their reaction time, and ensuring their fundamentals are second nature. However, as a lifelong Detroit Lions fan, I’m not sure this analogy is always accurate. While I love my Lions, there have been plenty of games where it looked like they just learned the plays in the huddle! But all joking aside, as educators, we are preparing our students for life skills, not just a state test.

The Problem: The “Skill Blur”

When students are sitting at a computer, facing math problems one after another, cognitive overload is a real threat. The “how and when” of the four operations can easily get jumbled with fraction rules, and suddenly, all that geometry vocabulary becomes one big ole mess in their heads. This can be frustrating for both students and teachers.

It’s not that they didn’t learn the material; it’s that the retrieval is getting blocked by the sheer volume of information and tasks that need to be completed.

The Solution: MathReps as a Tactical Warm-Up

MathReps lower the affective filter by repeatedly practicing these core skills. I remember a year when my students didn’t just “do a unit” on decimals; we consistently spiraled decimal practice into our MathReps alongside other skills.

Because it was part of their regular routine, when they eventually faced a screen with decimal problems and tasks at the end of the year, they didn’t panic. The decimal didn’t throw them because it wasn’t a “guest star” in the curriculum; it was a familiar friend. By using MathReps as a 10-minute daily “Tactical Warm-Up,” we help students:

  1. Filter out the Format: They’ve seen the area model and the number line hundreds of times. The “test screen” is just another canvas for their existing skills.
  2. Sharpen the Fundamentals: We move from “manual labor” math to automaticity.

The 15-Day “Polishing” Routine

If you have 15 days left before the test, don’t reach for a packet. Reach for a Routine or EduProtocol.

  • The Selection: Pick the MathRep that addresses the skill your students find the weakest. If they are tripping over the arithmetic, use an Operations Frame (like the giraffe example below).
  • The Routine: Use the same MathRep at the beginning of your math period for at least one week. Consistency beats variety here. On Day 1, they are reacquainting themselves with the procedures; by Day 5, they are mastering the logic.
  • The Pivot: After 5 days, if you’re feeling good, move to another high-leverage frame. Or, cycle back to a different MathRep you used earlier in the year to keep those older skills from getting lost in the sauce.

The Bottom Line

We aren’t “cramming” for a test; we are clearing the fog. When we polish these skills through MathReps, we give students the confidence to show what they actually know, rather than getting lost in the “mess” of a testing interface and the information overload that bogs them down.

What Science Says About Technology

Admin1 Comment

As we continue this series, it’s important to ground our reflections in the science of learning and brain research. Teachers make daily instructional decisions that research can illuminate but not fully prescribe. What neuroscience and educational science show us are principles that help explain how students learn best and how certain practices support long-term understanding. Previous post

Active Retrieval Is More Powerful Than Passive Re-Exposure

Cognitive psychology has consistently found that retrieval practice, that is, actively bringing information to mind, deepens learning more than simply re-reading or re-exposure. Research spanning laboratory and classroom settings shows that engaging students in retrieval (quizzing, explaining, recall exercises) leads to better long-term memory retention than repeated study or review alone. (source 1, Source 2)

This is often referred to as the testing effect or retrieval practice effect. The retrieval practice effect is an effective strategy for combating the Ebbinghaus Effect, aka the Forgetting Curve. While it is sometimes misinterpreted as “more tests,” it is really about effortful recall, getting students to retrieve and rethink information. It’s retrieval itself, not just repetition, that strengthens memory traces.

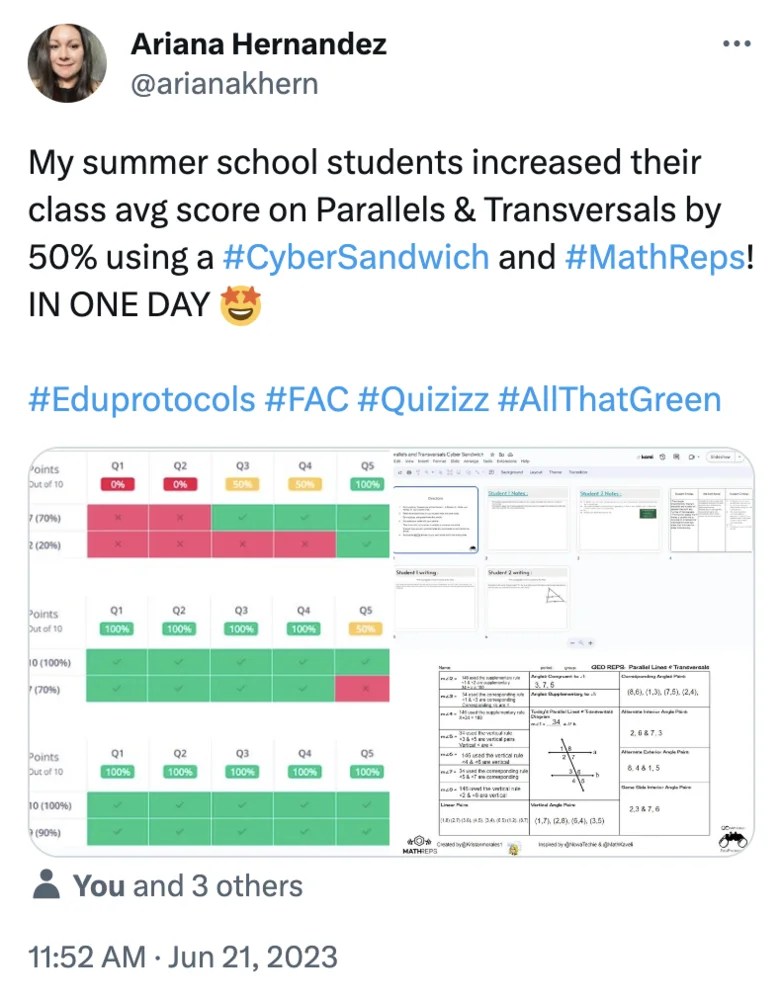
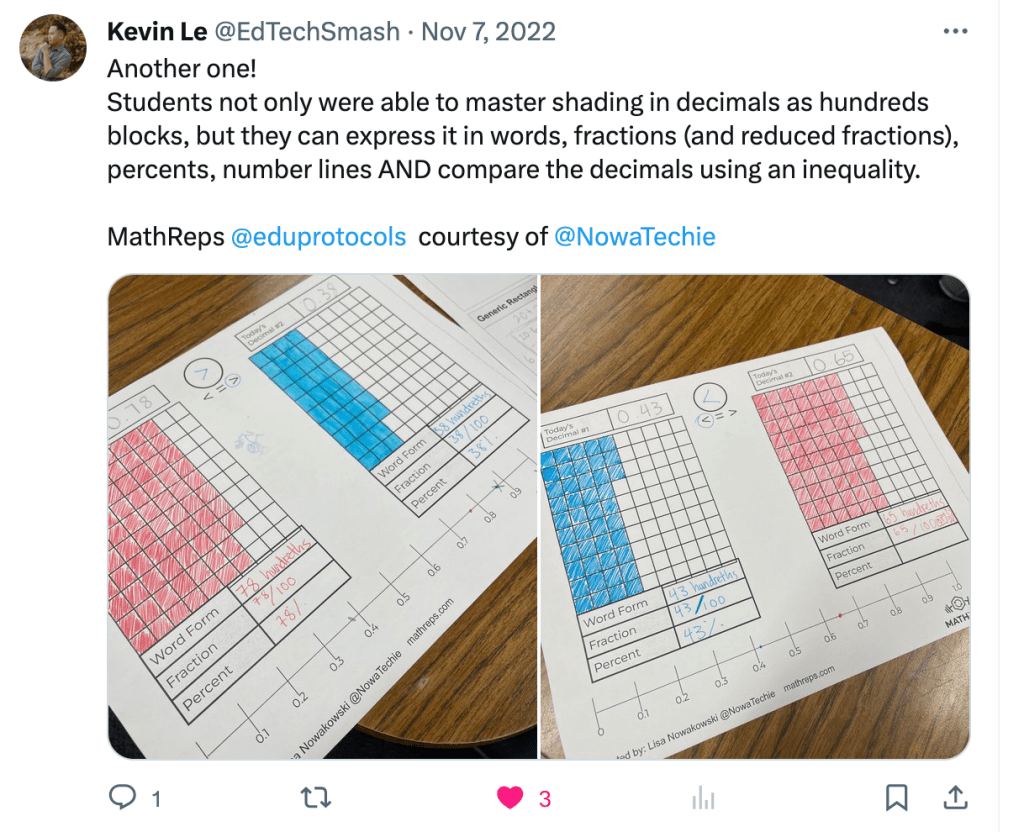
In other words, this means that asking students to produce explanations, to summarize in their own words, or to write and discuss thinking aloud builds deeper learning than simply having them repeatedly read material or answer DOK 1-type questions. This aligns closely with production-based approaches like #MathReps and #EduProtocols, which encourage students to reveal their thinking rather than simply select answers.

Cognitive Load Matters Both With and Without Screens

Science also reminds us that our brains have limited working memory capacity. Cognitive Load Theory explains that when students are overwhelmed with too much information or poorly structured tasks, learning suffers. This is why #EduProtocols recommends starting with a fun, low-cognitive load (non-academic) subject when introducing a new protocol.

Some research on multimedia learning, how information is presented with visuals, audio, and text, suggests that poorly designed digital content can increase cognitive load, making it harder for students to focus on what matters.

Importantly, cognitive load is not caused by screens themselves, but by how information is presented and how much unrelated or distracting material competes for attention. Even when we don’t use technology, we have all experienced cognitive overload from information, especially when it is new or ‘meaty’. This is why it is important to use well-designed tasks that chunk information, reduce unnecessary complexity, and scaffold thinking, helping students allocate mental energy to deep learning, whether on paper or on a device.

This is where tech can help: platforms that analyze student errors, present information in multiple representations, or guide students through step-by-step reasoning can reduce unnecessary load and help students focus on what matters most. Tools like Snorkl and Wayground (which provide instant feedback and class-wide analysis) can lighten the teacher’s load while still requiring students to produce and explain their thinking. This isn’t to say that the use of technology is better. If a teacher needs to learn a platform to lighten their load, it can lead to cognitive overload; that’s not good either.

It’s about balance for both students and teachers.

Explanation Strengthens Learning Across Contexts

Research and classroom evidence agree upon a central idea: students learn better when they must explain their thinking. This is true whether explanations are verbal, written, visual, or recorded. Explanation forces students to organize, articulate, and refine their understanding, something that passive or consumption tasks rarely do.

This finding is supported by the English Language Development (ELD) standards, which highlight explanation as crucial for language learners; I would argue the same holds for all students. The act of explaining requires higher-order thinking, connecting ideas, making meaning, and justifying reasoning, and is linked to stronger understanding across domains. We know that if a student can accurately explain their thinking, they understand the concept. And if, while they explain their thinking, they have a misconception, we, as teachers, can address the issue immediately.

Whether students are explaining mathematical reasoning, composing a paragraph, or teaching a peer through a screencast, the cognitive work of explanation activates deeper learning processes.

What Neuroscience Says About Screen Use

Neuroscience research and cognitive development studies paint a layered picture of screen use, especially in early childhood and developing brains. As teachers, we have all seen our fair share of young children passively watching something on a phone or tablet. I have my own personal thoughts on that.

Some findings suggest that excessive screen time, especially passive, unstructured exposure, can be associated with reduced development of executive functions (such as working memory, inhibitory control, and attentional networks) and changes in brain connectivity during critical developmental periods. (Source 3) Other work points out that heavy screen exposure in young children can replace activities like conversation, play, and social interaction that are essential for the development of attention, language, and executive skills. (Source 4)

I will acknowledge the limits of this research:

  • Most studies on screen use and brain development focus on quantity and context of use, not technology per se.
  • Research does not support simplistic claims that screens alone “ruin attention” or permanently damage cognition; effects depend heavily on the type of engagement, content quality, and context. (Source 5)
  • There is no consensus that screens are inherently worse for learning than other media; rather, the design of tasks and interactions matters most. I would be curious to see any studies on the effects of social media on attention spans, how they relate to perseverance and productive struggle.

Screens can be part of effective learning when they prompt students to think, produce, interact, and explain, not just watch or click. I still advocate for common sense. Personally, I don’t think plunking students down in front of a computer for extended periods of time every day is healthy.

What Research Doesn’t Claim

As educators, we must be careful not to overinterpret research into simple slogans like “technology is harmful” or “screens destroy brains.” The science shows that how we use technology matters far more than whether it exists in the classroom.

Studies on cognitive load don’t condemn all digital tools. They simply remind us that well-designed tasks that minimize the load and maximize meaningful engagement lead to better outcomes.

It’s all about balance.

What This Means for Classrooms

The science of learning supports production-based work, tasks that get students to retrieve, organize, and explain content. It also supports varied modalities and repetitive practices, whether via paper/pencil or smart tools that help with feedback and analysis. This was discussed in the Consumption vs Production post of this series.

Here’s what teachers and leaders should keep in mind:

  • Retrieval practice (active recall) strengthens long-term retention more than repeated exposure.
  • Cognitive load matters: thoughtful design matters more than screens.
  • Explanation builds understanding: making students’ thinking visible is powerful.
  • Tech can help, but only when it supports thinking, not replaces it.

Tools like Snorkl and Wayground illustrate this well: they can provide instant feedback and class analysis, helping teachers target instruction while students practice articulation of thinking. But these tools are most effective when teachers know what they want students to produce, not just consume.

Educators deserve systems that support this deeper work—not just devices to fill time. They also need support to accomplish this successfully. Leaving teachers to figure things out on their own time isn’t an acceptable solution. Schools and districts need to invest in their teachers.

What are your thoughts on this research? What have your experiences been?

Coming Next:
Research may tell us what works, but oftentimes, teachers are left to figure out how to put it all into practice successfully. Post 4 explores what happens when pedagogy is expected without proper time, training, or systemic support.