MLRs

Mastering Mathematical Language Routine 7: Compare and Connect

Image AdminLeave a comment

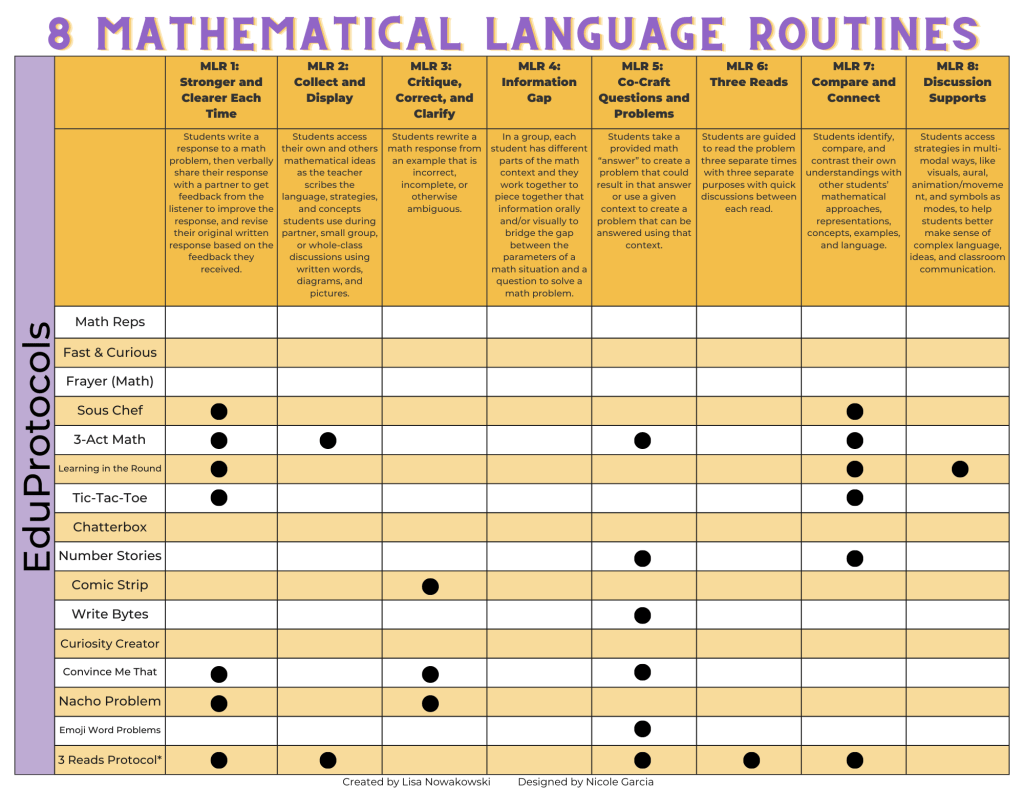
In the previous Mathematical Language Routine (MLR) discussions, we explored a variety of essential skills. MLR 1 focused on enhancing our understanding by revisiting and reinforcing key concepts, making our knowledge “Stronger and Clearer Each Time.” We then moved on to MLR 2, where we delved into the crucial skill of “Collecting and Displaying” data effectively. Building on this foundation, MLR 3 emphasized the importance of “Critiquing, Correcting, and Clarifying” our models and methodologies for optimal results. In MLR 4, we explored the “Information Gap” and how to use this strategy to be thoughtful of the information needed to solve problems. Continuing this journey, MLR 5 introduced the skill of “Co-Crafting Questions and Problems” collaboratively to foster innovative approaches and insights. Finally, in MLR 6, we explored the technique of “Three Reads,” emphasizing the significance of multiple reads in order to enhance student understanding. Let’s now embark on our next MLR discussion, MLR 7 Compare and Connect.

MLR 7: “Compare and Connect,” has the purpose of fostering students’ meta-awareness in their exploration of different mathematical approaches, representations, concepts, examples, and language. Through this MLR, students are encouraged to reflect on and verbally respond to these comparisons. This involves analyzing why certain mathematical actions or statements are done in a particular way, identifying and explaining connections between various mathematical representations or methods, and pondering how one idea relates to others in terms of both concepts and language. To support this learning process, teachers should model their thinking aloud when addressing these questions. This routine allows students to engage in rich mathematical conversations. We will explore two ways in which to accomplish this.

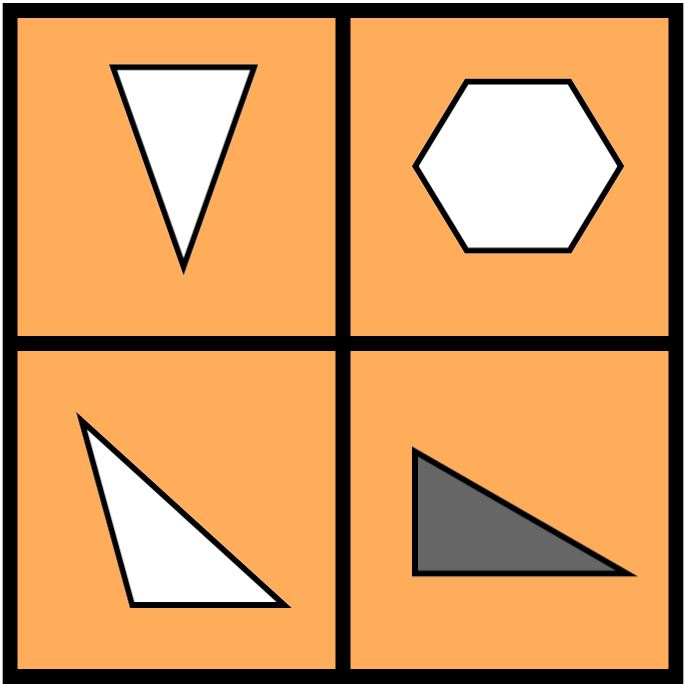
Which one doesn't belong

Getting students to engage in discussions about math, make connections, and consider different perspectives can be quite challenging. I often encounter students who simply say, “It was in my brain” or “My brain told me the answer.” However, by modeling and encouraging metacognitive awareness, students can begin to make connections on their own. One effective routine that focuses on linguistic skills is called ‘Which One Doesn’t Belong‘. This activity can be done in groups, in pairs, or as a whole class. Students are presented with four images, equations, numbers, graphs, or geometric shapes, and they are asked to identify a commonality among three of them and explain their reasoning. The interesting twist is that any combination of three out of the four options can be correct. For example, in the orange example, one could argue that the three triangles go together and the hexagon is the odd one out. Alternatively, one could justify grouping all the white-filled shapes while excluding the shaded shape. This activity is both enjoyable for students and provides the opportunity to hear and consider different viewpoints.

Another interesting activity that aligns well with this MLR is the Math EduProtocol Sous Chef from The EduProtocols Field Guide Math Edition (Chapter 9, page 56). In this activity, students are grouped together to solve a problem using different approaches and then present their work to the class. For instance, if students were given the task of solving 4 x 6 in third grade, one student might use equal groups, another could opt for repeated addition, a third student may create an array, while the last student represents the equation with the area model. Through this activity, students can establish connections with previously learned concepts and broaden their understanding. There are numerous ways to implement Sous Chef, but the central focus remains on fostering connections among ideas and encouraging students to share their thought processes orally.

In conclusion, incorporating this MLR into your math class will greatly benefit your students. It will help them enhance their meta-awareness, make connections between different concepts, and foster a deeper understanding of the subject. While we have explored two approaches to this MLR, there are numerous other equally powerful techniques available. In our next discussion, we will delve into MLR 8: Discussion Supports, which focuses on stimulating rich and meaningful conversations in the classroom.

Mastering Mathematical Language Routine 6: Three Reads

Image Admin2 Comments

In our recent posts, we have explored various Mathematical Language Routines (MLRs) that aim to foster language development in the math classroom. We have covered MLR 1: “Stronger and Clearer Each Time,” MLR 2: “Collect and Display,” MLR 3: “Critique, Correct, Clarify,” MLR 4: “Information Gap,” and MLR 5: “Co-Craft Questions and Problems.” Each of these MLRs has offered valuable insights into different aspects of language acquisition in mathematics, be it written and oral expression, oral language proficiency, or the comprehension of tasks and word problems.

MLR 6: Three Reads

Building upon these discussions, let’s now delve into our next MLR, MLR 6: “Three Reads.” This routine plays a crucial role in enhancing reading comprehension and developing meta-awareness of mathematical language. By engaging in this exercise, students get the opportunity to practice navigating the intricacies of math-related questions, which often pose challenges for them. Through multiple readings, they can better understand the unique ways in which math concepts are presented and effectively plan their strategies for problem-solving. MLR 6: “Three Reads” serves as an important tool for supporting students’ grasp of mathematical language and equips them with the skills needed to tackle word problems with confidence.

The Three Reads protocol is a powerful tool designed to enhance students’ understanding of mathematical word problems. Its main purpose is to break down complex problems into manageable steps that students can comprehend, analyze, and solve successfully. This protocol is particularly beneficial for multilanguage learners and students with academic disabilities who often struggle with comprehending mathematical texts.

The Three Reads protocol begins by encouraging students to focus on the meaning of the problem. Instead of rushing to perform calculations, students are prompted to truly understand the context and situation described in the word problem. This initial step allows students to connect with the story or situation presented and reflect on its implications.

After gaining a solid understanding of the problem’s context, students move on to the second read. Here, they concentrate on identifying the units and quantities involved in the problem. By focusing on these key components, students can make sense of the mathematical concepts and relationships embedded within the word problem.

Finally, during the third read, students shift their attention to the specific tasks or questions asked in the problem. By this stage, students have already engaged deeply with the problem’s meaning and mathematical content. They are now able to formulate a plan of action and approach the problem in a strategic manner.

The Three Reads protocol supports not only reading comprehension but also sense-making and meaningful conversations around mathematical texts. By emphasizing understanding and meaning before diving into calculations, students are given the opportunity to reflect on different presentation styles, negotiate interpretations, and explore multiple solution strategies.

Let’s explore an example that demonstrates how to implement the protocol of co-crafting questions with students. In this example, Mateo’s M&Ms, the quantities are initially hidden to allow students to focus on comprehending the story. Once they grasp the concept that Mateo has a bag of M&Ms with different colors, the quantities are revealed. At this point, students can create a T chart to organize the quantities and their corresponding units. Although the units are the same in this particular example, it’s important to note that it may not always be the case in every word problem. Utilizing the T chart helps students effectively organize the information. Moving on, the final phase of this example involves students creating their own questions, reminiscent of MLR 5. By allowing students to differentiate and choose their own questions, they are encouraged to tackle more challenging problems rather than opting for the easy way out. This approach also fosters open-ended questions that lead to a variety of possible solutions. It’s a wonderful way to introduce this routine. Additionally, another teacher in my district, Nicole Garcia, and I have developed a recording sheet to assist students in organizing their thoughts and work. It’s worth noting that it’s also practical to address problems that already come with pre-established questions. In these cases, steps 1 and 2 of the protocol remain the same. However, in step 3, students formulate a plan to answer the provided question. Once again, reading the story multiple times allows students the necessary time to grasp and organize the given information.

Example of a 3 Reads

In summary, the Three Reads protocol encourages students to engage actively with mathematical questions, reflect on presentation styles, and negotiate meaning. By following this routine, students can develop a deeper comprehension of word problems, improve their mathematical reasoning skills, and ultimately enhance their overall problem-solving abilities.

Mastering Mathematical Language Routine 5: Co-Craft Questions and Problems

Image Admin1 Comment

In this ongoing blog series on Mathematical Language Routines (MLRs), we have covered four essential routines so far. Let’s recap their key ideas: MLR 1: “Stronger and Clearer Each Time,” MLR 2: “Collect and Display,” MLR 3: “Critique, Correct, Clarify,” and MLR 4: “Information Gap.” These routines are designed to enhance oral and written communication skills in mathematics. Now, let’s turn our attention to MLR 5: “Co-Craft Questions and Problems,” which offers a unique approach. It encourages students to actively participate in the question and problem-solving process, enabling them to explore mathematical contexts before seeking answers.

In MLR 5, students are given the opportunity to dive deeper into problem-solving by creating, analyzing, and enhancing mathematical questions, problems, and situations. The purpose of this routine is to provide students with a space where they can generate, analyze, and improve their understanding of mathematical concepts, specifically word problems. Through engaging in conversations, students refine their ability to formulate, select, and refine questions, allowing them to develop stronger critical thinking skills. This routine fosters students’ ability to use conversation skills effectively in the process of formulating, selecting, and refining their mathematical questions and problems. By actively participating in these conversations, students take ownership of their learning and become more proficient problem solvers. Curiosity Creator, found in The EduProtocols Field Guide Math Edition, Chapter 18, is one way to practice this routine.

Another excellent routine that can be seamlessly integrated into MLR 5 is the 3-Act Math Task, originally developed by Dan Meyer. This ingenious task involves providing students with minimal information, serving as a catalyst to foster curiosity and encourage them to generate questions that they can later answer with additional information provided in subsequent acts.


The first act, known as Act 1, is designed to stimulate students’ observation skills and curiosity. During this phase, students are encouraged to ponder upon what they notice and wonder about the given scenario. They also formulate questions that they will eventually solve. Act 1 is an opportune moment for students to engage in conversations regarding their observations, estimations ( too high, too low, or actual), a specific focus question, and the type of information they need to answer their own question.


In Act 2, students are provided with the necessary information to solve the problem or question they crafted in Act 1. Armed with this newfound knowledge, they embark upon the solving process.
Finally, Act 3 allows students to review the actual answer and assess whether their initial predictions were correct.

This routine is highly engaging for students across all levels, offering a perfect balance between accessibility and challenge. It also offers a wide range of ready-made, standards-aligned tasks suitable for students from Kindergarten through high school. By incorporating the 3-Act Math Task routine into the classroom, instructors can empower students to actively participate in problem-solving, develop critical thinking skills, and cultivate a deep understanding of the importance of co-constructing problems and questions.

Mastering Mathematical Language Routine 2: Collect and Display

Image Admin2 Comments

In the previous post, we delved into the significance of the Mathematical Language Routine 1 (MLR 1) “Stronger and Clearer Each Time.” MLR 1 focuses on nurturing a deeper understanding of mathematics by encouraging students to thoughtfully articulate their thinking process, either individually or in groups. Through explanation and attentive listening, students refine their writing skills and strive to explain concepts at a more profound level, akin to mathematicians.

Mathematical Language Routine 2: Collect and Display

Now, let’s turn our attention to MLR 2, known as “Collect and Display.” The primary objective of MLR 2 is to capture the oral language utilized by students during discussions, creating a valuable reference for later use. This capturing process encompasses various forms, including words, diagrams, and images. By collecting and displaying this language-rich content, MLR 2 aids students in establishing connections between different mathematical concepts, as well as facilitating the integration of academic language into their understanding and expression. Additionally, MLR 2 provides immediate feedback, an essential element in student learning, and offers a structured framework for self-reflection and language usage. Join along as we explore MLR 2 further in this post.

The focus of this routine is to collect students’ thoughts using verbal, pictorial, and diagrammatic representations. Although visuals play a role, they are not the main focus. The purpose is to explain the importance of using visual aids to collect and showcase student ideas in mathematics.

This routine aims to stabilize the ever-changing language used by students so that their own output can serve as a reference in developing their mathematical language. The teacher actively listens and records the language employed by students during discussions, whether it’s in pairs, small groups, or the entire class. This includes capturing written words, diagrams, and pictures.

The collected output can be organized, restated, or connected to other language in a display that all students can refer to, build upon, and make connections with during future discussions or writing activities. Throughout the unit, teachers can use the displayed language as a model, update and revise the display as student language evolves, and create connections between student language and new disciplinary language.

This routine provides valuable feedback to students, enhancing their understanding while simultaneously fostering their awareness of language.

When it comes to collecting data during student discussions in math class, there are effective strategies to encourage students to represent their mathematical thinking visually. One popular approach is incorporating Number Talks, a practice already utilized by many teachers. During Number Talks, teachers can record their methods and thoughts, which not only helps them make connections but also allows for discussions about the most efficient approaches. However, it’s important to note that sometimes students may overcomplicate their solutions to showcase the flexibility of their thinking. To address this, scribing these methods can help students realize the value of efficiency. Apart from Number Talks, there are other strategies to encourage visual representation of mathematical thinking. Teachers can introduce visual organizers like graphic organizers or mind maps, which help students organize and illustrate their ideas. Additionally, utilizing tools such as virtual or physical whiteboards or digital sketching apps can enable students to visually capture their thought processes. Activities like creating diagrams or pictures also enhance the collection of student ideas in a visual format, providing teachers with valuable insights into student understanding and promoting deeper mathematical thinking.

The method of collecting student data can vary depending on the teacher’s preference. Some teachers may opt for traditional methods like chart paper, prominently displayed in the classroom. Others may choose digital tools like Padlet. Regardless of the chosen method, the collected data will be easily accessible to students whenever they need it. It is encouraged for students to utilize these records when expressing their thoughts, whether orally or in writing. As a teacher, it is important to highlight this resource for students and demonstrate how to effectively utilize it.

In conclusion, we have explored the significance of MLR 2: “Collect and Display” in fostering effective language students use to communicate their mathematical thinking. This routine has proven to be a valuable tool for students, as it allows them to actively engage with mathematical concepts and communicate their ideas effectively. By collecting and displaying their thinking, students can enhance their understanding and learn from their peers. Moving forward, we will delve into MLR 3: “Critique, Correct, and Clarify” in our next blog post. Stay tuned as we continue to explore the power of Mathematical Language Routines in promoting mathematical discourse and deepening conceptual understanding.

Mastering Mathematical Language Routine 1: Stronger and Clearer Each Time

Image Admin2 Comments

Mathematical Language Routines (MLRs) play a crucial role in enhancing students’ comprehension and communication skills in mathematics. Developed to meet the diverse language needs of learners, these frameworks have become an invaluable tool in promoting a deeper understanding of mathematical concepts. In this series, we will explore each MLR in detail, starting with MLR 1: “Stronger and Clearer Each Time.”

Mathematical Language Routine 1: Stronger and Clearer Each Time

MLR 1: “Stronger and Clearer Each Time” focuses on refining students’ ideas and communication through various activities. By incorporating writing, listening, explaining, and integrating new language, students are encouraged to continually improve their understanding of mathematical concepts. This routine, often conducted in pairs, provides students with the opportunity to collaborate and build upon each other’s ideas, fostering a culture of shared learning and growth.

Throughout this series, we will delve into the different structures and strategies that can be employed within MLR 1, unveiling how this routine nurtures students’ confidence and fluency in mathematics. Join us as we explore the remarkable impact of MLR 1 and its profound influence on students’ language development and mathematical achievements.

The purpose of this routine is to foster the refinement of students’ verbal and written output through structured conversation and revision. By engaging in this process, students can enhance both their thinking and their expression of it.

In this routine, students initially work individually or in groups, gradually progressing towards partner work. This approach allows students to acclimate to the task and build their confidence. For those who may be less familiar with writing, explaining, and refining their thoughts, supportive strategies can be implemented to ensure their success.

Once the structures are in place, it is crucial for students to recognize the ultimate goal, which is either a deep understanding of the concept or the ability to articulate it like an expert. The listener’s role becomes significant as they ask clarifying questions, enabling a comprehensive understanding of the speaker’s thoughts. Simultaneously, the speaker benefits from this exchange, refining their thinking more clearly.

To encourage thorough responses, it is valuable to have students switch partners multiple times during the routine. By engaging in back-and-forth conversation, with equal emphasis on speaking and listening, students not only refine their thoughts but also strengthen their language and reasoning skills. The iterative nature of this process reinforces the importance of pressing for details and encourages the continual refinement of ideas.

Convince Me That, by Daniel Kaufmann, is a highly effective protocol that teachers can implement in their math lessons to foster deeper understanding and engagement among students. To successfully introduce and implement this routine, educators can follow these step-by-step guidelines:

  1. Introduce the Problem: Begin by presenting a math problem along with its solution to the students. For instance, students can be asked to explain why 3 x 4 equals 12.
  2. Form Partners or Small Groups: Divide the students into pairs or small groups to facilitate collaborative learning. This structure encourages peer interaction and promotes the sharing of ideas.
  3. Restrict Algorithmic Thinking: Emphasize that students should focus on concrete or pictorial methods rather than relying on algorithms. This restriction encourages students to think deeply about the problem and explore alternative approaches.
  4. Initiate Individual Thinking: Give students time to think individually about the problem and develop their own explanations for the solution. This step helps to build independence and promotes critical thinking skills.
  5. Structured Pairing: After individual thinking, partners or group members should share their explanations with each other. This process enables students to refine their understanding through constructive discussions and peer feedback.
  6. Revise Written Responses: Encourage students to revise and improve their written explanations based on the feedback received during the structured pairing phase. This step promotes self-reflection and reinforces learning.

To facilitate the refinement process and prompt students effectively, here are some examples suitable for Math Learning Routine (MLR) 1:

  • “Convince your partner why the sum of any two even numbers is always even.”
  • “Explain to your group why dividing by zero is undefined and cannot result in a finite number.”
  • “Justify why the product of any number and zero is always zero.”

These prompts stimulate students to think critically, apply their knowledge, and refine their explanations. By implementing the Convince Me That routine with these strategies and prompts, educators can foster deeper conversations, encourage active learning, and enable students to demonstrate a more profound understanding of mathematical concepts.

For a more detailed explanation and implementation guidelines, you can refer to Chapter 19 of The EduProtocols Field Guide Math Edition. This invaluable resource offers comprehensive insights and practical tips for effectively utilizing the Convince Me That routine in math classrooms.

In conclusion, the implementation of MLR 1 has proven to be highly beneficial for students. It provides them with a structured platform to refine their thinking, improve their communication skills, and deepen their understanding of the subject matter. By engaging in the collaborative and iterative process of MLR 1, students are empowered to develop clearer and more coherent responses.

We invite you to stay engaged with our series and continue exploring the world of Mathematical Language Routines. The second routine in our series, MLR2: “Collect and Display”, has a specific purpose. It aims to capture students’ oral words and phrases and transform them into a stable, collective reference. The main goal is to preserve the language that students use and use it as a reference point for developing their mathematical language.

Enhancing Math Discourse: Introducing the ‘Mastering Mathematical Language Routines’ Series

Image AdminLeave a comment

Unleash the Power of Mathematical Language: Introducing the Game-Changing 8 Routines

Calling all educators! Prepare to embark on a transformative educational journey unlike any other. I am thrilled to bring you a powerful series on Mathematical Language Routines – the game-changers that will revolutionize your math classroom. Crafted by the brilliant minds at Stanford University and wholeheartedly adopted by the esteemed CA Department of Education in the newly adopted 2023 Math Frameworks, these routines are set to redefine the way we teach and learn mathematics.

But what exactly are these Mathematical Language Routines? There are eight carefully designed techniques that provide a powerful framework for enhancing language acquisition in the context of mathematical learning. These routines have proven to be instrumental in bridging the gap between mathematics and language, ensuring that students develop a deep understanding of both. Throughout this captivating series, we will delve into each routine, unpacking their unique benefits and offering practical guidance on how to implement them effectively in your classroom.

In this series, we will delve into 8 Mathematical Language Routines (MLRs) that can effortlessly enhance your math classroom experience, no matter the age group you teach. Let’s start with

MLR 1: Stronger and Clearer Each Time – In this routine, students write and share their responses to math problems verbally. They eagerly listen to valuable feedback, which further enriches and refines their responses.

MLR 2: Collect and Display – As students explain their thoughts and processes, the teacher captures the language they use. This serves as a helpful tool for further clarification.

MLR 3: Critique, Correct, and Clarify – Think of this as an in-depth analysis of errors to enhance learning.

MLR 4: Information Gap – Students form two groups, each with partial information, and must collaborate to solve a problem by obtaining the missing pieces of information.

MLR 5: Co-Craft Questions and Problems – Here, students generate questions and problems based on real-life scenarios, akin to the engaging nature of 3-Act Math Tasks.

MLR 6: Three Reads – This routine involves reading a problem three times, each time with a specific purpose. It is particularly effective for dissecting story or word problems.

MLR 7: Compare and Connect – Students compare, discuss, and connect their understandings with those of their peers.

MLR 8: Discussion Supports – Supportive sentence frames, thoughtfully organized into categories, can enhance students’ participation in discussions.

Get ready to embark on an exciting journey that will revolutionize your teaching practice. Together, we will explore the immense potential of these MLRs, empowering you to unleash the true capabilities of your students in mathematics and beyond. Over the past two years, I have gathered a wealth of knowledge in this area, and I can’t wait to share it with you. Join me as we dive into this exhilarating series, equipping you with the tools and skills to excel, ensuring your students’ success. Come back for more captivating insights that will leave you inspired and eager for the next installment.