Unleash the Power of Mathematical Language: Introducing the Game-Changing 8 Routines
Calling all educators! Prepare to embark on a transformative educational journey unlike any other. I am thrilled to bring you a powerful series on Mathematical Language Routines – the game-changers that will revolutionize your math classroom. Crafted by the brilliant minds at Stanford University and wholeheartedly adopted by the esteemed CA Department of Education in the newly adopted 2023 Math Frameworks, these routines are set to redefine the way we teach and learn mathematics.
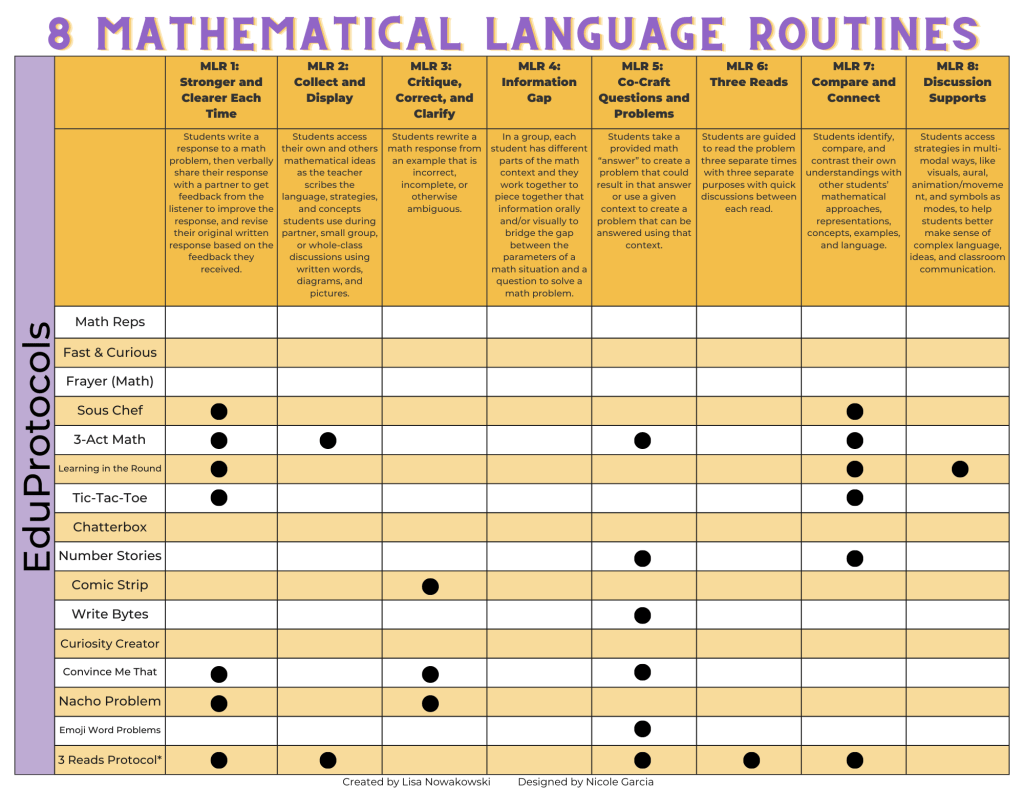
But what exactly are these Mathematical Language Routines? There are eight carefully designed techniques that provide a powerful framework for enhancing language acquisition in the context of mathematical learning. These routines have proven to be instrumental in bridging the gap between mathematics and language, ensuring that students develop a deep understanding of both. Throughout this captivating series, we will delve into each routine, unpacking their unique benefits and offering practical guidance on how to implement them effectively in your classroom.
In this series, we will delve into 8 Mathematical Language Routines (MLRs) that can effortlessly enhance your math classroom experience, no matter the age group you teach. Let’s start with
MLR 1: Stronger and Clearer Each Time – In this routine, students write and share their responses to math problems verbally. They eagerly listen to valuable feedback, which further enriches and refines their responses.
MLR 2: Collect and Display – As students explain their thoughts and processes, the teacher captures the language they use. This serves as a helpful tool for further clarification.
MLR 3: Critique, Correct, and Clarify – Think of this as an in-depth analysis of errors to enhance learning.
MLR 4: Information Gap – Students form two groups, each with partial information, and must collaborate to solve a problem by obtaining the missing pieces of information.
MLR 5: Co-Craft Questions and Problems – Here, students generate questions and problems based on real-life scenarios, akin to the engaging nature of 3-Act Math Tasks.
MLR 6: Three Reads – This routine involves reading a problem three times, each time with a specific purpose. It is particularly effective for dissecting story or word problems.
MLR 7: Compare and Connect – Students compare, discuss, and connect their understandings with those of their peers.
MLR 8: Discussion Supports – Supportive sentence frames, thoughtfully organized into categories, can enhance students’ participation in discussions.
Get ready to embark on an exciting journey that will revolutionize your teaching practice. Together, we will explore the immense potential of these MLRs, empowering you to unleash the true capabilities of your students in mathematics and beyond. Over the past two years, I have gathered a wealth of knowledge in this area, and I can’t wait to share it with you. Join me as we dive into this exhilarating series, equipping you with the tools and skills to excel, ensuring your students’ success. Come back for more captivating insights that will leave you inspired and eager for the next installment.