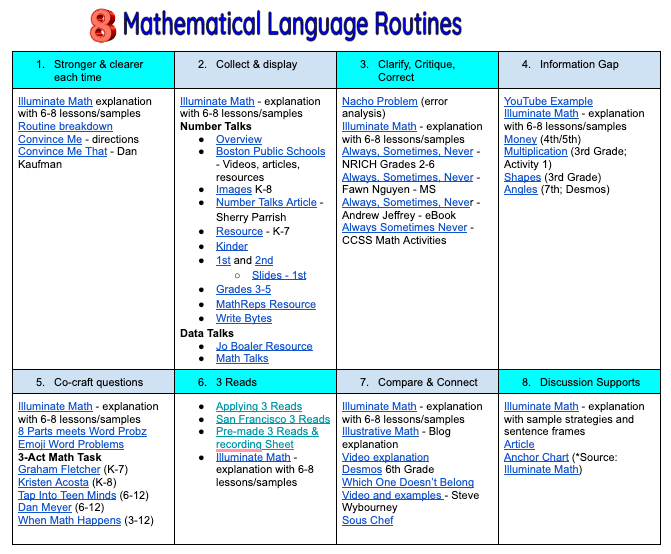
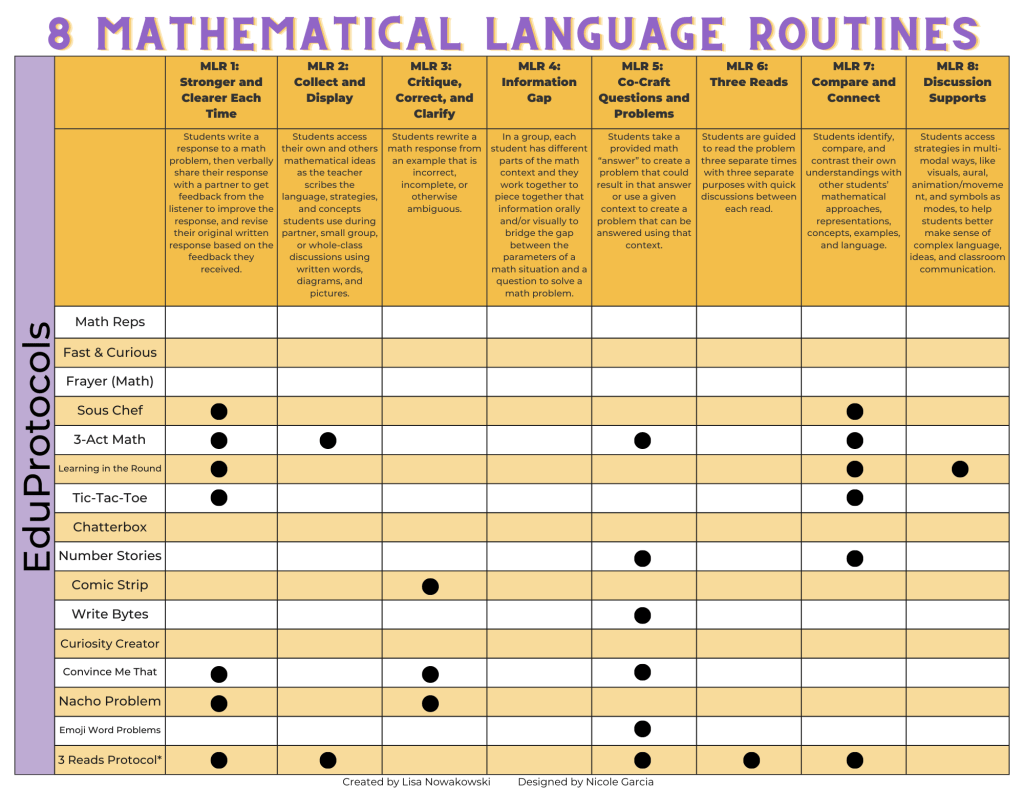
Looking back at the series of Mathematical Language Routines (MLRs) we have explored, we can see that their collective aim is to foster robust mathematical discussions and enhance language proficiency among students. These routines serve diverse purposes, such as refining ideas through structured conversation (Stronger and Clearer Each Time), stabilizing oral language as a reference (Collect and Display), refining written arguments through critique (Critique, Correct, and Clarify), promoting collaborative problem-solving through information sharing (Information Gap), empowering students to craft mathematical questions (Co-Craft Questions and Problems), facilitating comprehension and negotiation of math texts (Three Reads), and encouraging comparison and connection between various mathematical approaches and representations (Compare and Connect). Together, these MLRs not only elevate student participation and conversation but also cultivate meta-awareness of language, fostering a deeper understanding of mathematical concepts.

We conclude this series with Mathematical Language Routine 8: Discussion Supports. The goal is to foster inclusive discussions in math by combining multi-modal strategies that aid in understanding complex language, ideas, and classroom communication. These strategies encourage student participation, conversation, and awareness of language nuances. With continued modeling, the aim is for students to adopt these techniques independently, prompting deeper engagement among peers in discussions.

Having rich mathematical discussions can be challenging, especially when there are barriers that hinder effective communication. Recently, I encountered a situation where I was assisting a student with a math problem. The task was to determine the combination of rolls of coins needed to reach a specific amount. The problem provided information about the rolls of nickels and dimes, including the quantity each roll contained. However, during our discussion, it became evident that the student misunderstood the task. They believed they needed to determine the number of dimes or nickels in each roll, rather than finding the overall combination. To clarify this confusion, I decided to show them an image of a roll of coins and briefly discussed its concept, which helped them grasp the correct approach. This incident highlighted the importance of uncovering and addressing any gaps in background knowledge. It also underscored the significance of reflecting on the relevance of certain questions.

Having sentence frames is not only helpful to me but also to the students. The above image is one that I created based on Illuminate Math‘s suggestions. These sentence frames can guide the class towards deeper thinking and understanding. As mentioned before, the main objective of this routine is to encourage students to take the lead in these discussions. Additionally, it is important to note that this particular routine can be integrated into any of the other Mathematical Learning Routines (MLRs).

This concludes our multi-part series on the 8 Mathematical Routines. I highly encourage you to start implementing these routines in your day-to-day math class. To further support you on this journey, I have gathered a variety of helpful resources, which you can access here. If you have any additional resources to share, please don’t hesitate to reach out. I will gladly add them to the collection and give you proper credit.

Recap of the previous MLR discussions: We have reached the halfway point in the series of Mathematical Language Routines (MLRs). So far, we have explored MLR 1: “Stronger and Clearer Each Time,” where the focus was on enhancing understanding and communication skills through the use of the “Convince Me That” technique. This was followed by MLR 2: “Collect and Display,” which aimed at expanding students’ academic vocabulary. MLR 3: “Critique, Correct, Clarify” was centered around improving both oral and written skills, utilizing the EduProtocol Nacho Problem. Now, let’s introduce MLR 4: “Information Gap,” a personal favorite, which promotes collaborative work and helps students identify critical information necessary for solving word problems. This routine plays a vital role in fostering meaningful interactions and communication in the realm of mathematics.

One of the biggest issues in math classrooms is the challenge of word problems, also known as story problems. These problems require students to go through multiple steps, including reading comprehension, deciphering the question, creating a plan, and solving the problem. However, students often struggle with knowing how to use the given information and which details are relevant to the solution.

To address this problem, Information Gap tasks have been developed to help students navigate this challenge. In these tasks, students are divided into two groups: one group has the data card, while the other group has the problem card.

The group with the problem card reads the problem silently and asks the group with the data card for the information necessary to solve the problem. It’s important that neither group shows their cards to the other. Before sharing the information, the group with the data card asks the problem group why they need that specific information. This process encourages the problem group to justify their reasoning and ensures that they have thoroughly thought out the solution process.

This collaborative process continues until all the required information is obtained. Once both groups have shared their cards, they can work together to solve the problem. The goal of this approach is to create a need for students to communicate and collaborate, as this type of task cannot be accomplished alone.

When starting this process, it is beneficial to demonstrate it to the class. Initially, I present the problem card to the entire class while holding the data card myself. I then instruct students to work in pairs and determine what information they need. They are encouraged to formulate questions to obtain the necessary information and provide a rationale for why they need it. I repeat this process several times until the entire class understands their roles. Gradually, I reduce the group size over time until they are working in pairs to complete this task. This routine helps students to slow down and approach their thinking more deliberately.

In summary, Information Gap tasks are designed to promote collaboration and problem-solving skills among students. By requiring them to share different pieces of information both orally and visually, these tasks facilitate effective communication and enhance their ability to work together towards a solution.

In the upcoming post, we will delve into MLR 5: Co-craft questions, where we explore how 8 P*Arts meets Word Problems, 3-Act Math Task, and Emoji Word Probz perfectly align with this approach. Join us in the next installment of the series to discover exciting examples and techniques that will surely ignite your interest and leave you eager to come back for more. Stay tuned!